デロイト トーマツ イノベーションパーク（東京都・丸の内）のショーケースをお借りして、羽ばたき飛翔ロボット「WiFly」の常設展示を開始しました！
場所はＪＲ東京駅・丸の内南口から徒歩５分、ＪＲ有楽町駅・国際フォーラム口から徒歩３分の新東京ビル８階。無料会員登録で誰でも利用可能なスペースで展示しています。
WiFlyショーケース出展中！
月別アーカイブ: 2024年7月
再考：ドライ酸化の初期異常
完全拡散律速成長モデルでは、ドライ酸化にみられる初期異常の解釈がDeal-Groveモデルの場合と１８０度変わります。今回は、このことを詳しく見ていきましょう。
下図は、Deal-Groveモデルと完全拡散律速モデルを並べて比較したものです。微分方程式の概形は全く同じで、放物型定数\(B\)も同じ。違うのは定数\(A\)ですが、
$$\kappa \equiv \frac{D_0}{L\int_{x_0-L}^{x_0}\exp\left [\frac{\Delta E(x)}{k_BT}\right ]dx-L}\label{kappa}\tag{1}$$
とおけば、線形速度定数\(B/A\)の式もDeal-Grove方程式と見た目が一緒になります。「完全拡散律速モデルといっても単に界面反応速度定数\(k\)の解釈を変えただけで、何も新しくないじゃないか」と批判されてしまいそうですが・・・、果たしてそうでしょうか？
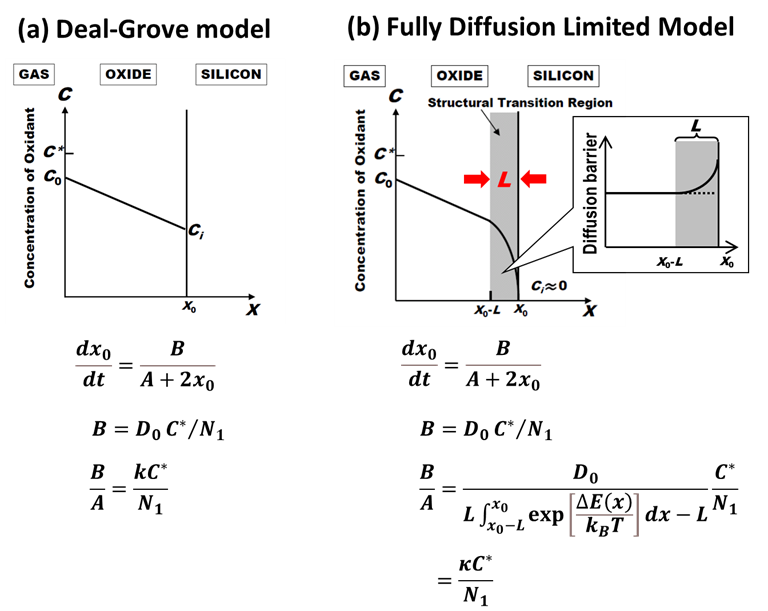
重要な変更点は、式\(\eqref{kappa}\)の速度定数\(\kappa\)が拡散係数\(D_0\)に比例するようになった点です。これにより、ドライ酸化にみられる初期異常の解釈がDeal-Groveモデルと変わってくるのです。
「Fargeixの解析」の回で、ドライ酸化の初期異常は、界面反応速度定数\(k\)が大きくなるか、あるいは拡散係数\(D_0\)が初期段階で低下していないと説明できない、という話をしました。DealとGroveは1965年の論文[1]で初期増速拡散説を唱えましたが、1983年のこのFargeixの解析[2]で否定されてしまったのです。
ところが、完全拡散律速モデルでは、この初期増速拡散説が復活します。Fargeixの解析にしたがって、酸化速度の逆数\(dt/dx_0\)の振る舞いを調べてみましょう。拡散係数\(D_0\)が酸化膜厚\(x_0\)に依存するとして、\(dt/dx_0\)を酸化膜厚\(x_0\)で微分すると
$$\begin{eqnarray}\frac{d}{dx_0}\left ( \frac{dt}{dx_0}\right ) &=&\frac{d}{dx_0}\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\\&=&\frac{d}{dx_0}\left ( \frac{A}{B}\right ) +\frac{d}{dx_0} \left (\frac{2}{B}\right )x_0+\frac{2}{B}\\&=&-\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\frac{1}{D_0} \frac{dD_0}{dx_0}+\frac{2}{B}\end{eqnarray}$$
となります。最後の式の第１項
$$-\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\frac{1}{D_0} \frac{dD_0}{dx_0}$$
が初期異常による、線形-放物型曲線からのずれに相当します。Fargeixが示したように、酸化速度の逆数\(dt/dx_0\)の勾配は\(x_0\rightarrow 0\)で増大しますので、\(dD_0/dx_0 <0\)でないといけません。つまり、酸化膜厚が薄くなるほど\(D_0\)が増大しなければ初期異常を説明できなくなるのです。これはDeal-Grove方程式とは真逆の結論です。
[1] B. E. Deal, A. S. Grove, J. Appl. Phys. 36, 3770 (1965).
[2] A. Fargeix, G. Ghibaudo, G. Kamarinos, J. Appl. Phys. 54, 2878 (1983).
完全拡散律速モデル（３）
前回新たに導出した定式化した式をつかって、酸化速度の実験値を再現するような構造遷移領域の厚さ\(L\)を求めてみましょう。
新しい酸化速度方程式では、定数\(B\)はDeal-Grove方程式と一緒ですが、定数\(A\)は
$$A= 2L\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx-2L+2D_0/h\label{a}\tag{1}$$
のように、構造遷移領域の厚さ\(L\)と構造遷移領域内の拡散障壁の増分\(\Delta E(x)\)に依存します。様々な温度における\(A\)の実験値がDeal-Groveの論文[1]に載っていますから、\(\Delta E(x)\)を適当に仮定すれば、実験値から\(L\)を求めることができます。
式\(\eqref{a}\)の中で、\(2D_0/h\)は無視します。酸化膜中の酸化種の拡散係数\(D_0\)と比べて、気相物質輸送係数\(h\)の方が圧倒的に大きいからです。DealとGroveの論文[1]でもそう仮定して解析していますし、この仮定は全く問題ありません。
また、\(\Delta E(x)\)ですが、線形速度定数\(B/A\)の活性化障壁が2eVなので、SiO2/Si界面における拡散障壁が約2eVになっていると考えると、\(\Delta E(x_0)\)は活性化障壁2eVから、界面から十分離れた酸化膜中の拡散障壁1.24eVを引いた値となるので
$$\Delta E(x_0) = 2.0 – 1.24 = 0.76 ({\rm eV})$$
とおけます。
下の表に、\(\Delta E(x)\)の関数形をいくつか適当に仮定して計算した、定数\(A\)の実験値を再現する\(L\)の値を示します。温度によって変わりますが、概ね1nm弱になっていることがわかります。いろいろな実験で指摘されていた、SiO2/Si界面近傍の構造遷移領域の厚さと一致しているので、この完全拡散律速モデルの妥当性を裏付けていると言えるでしょう。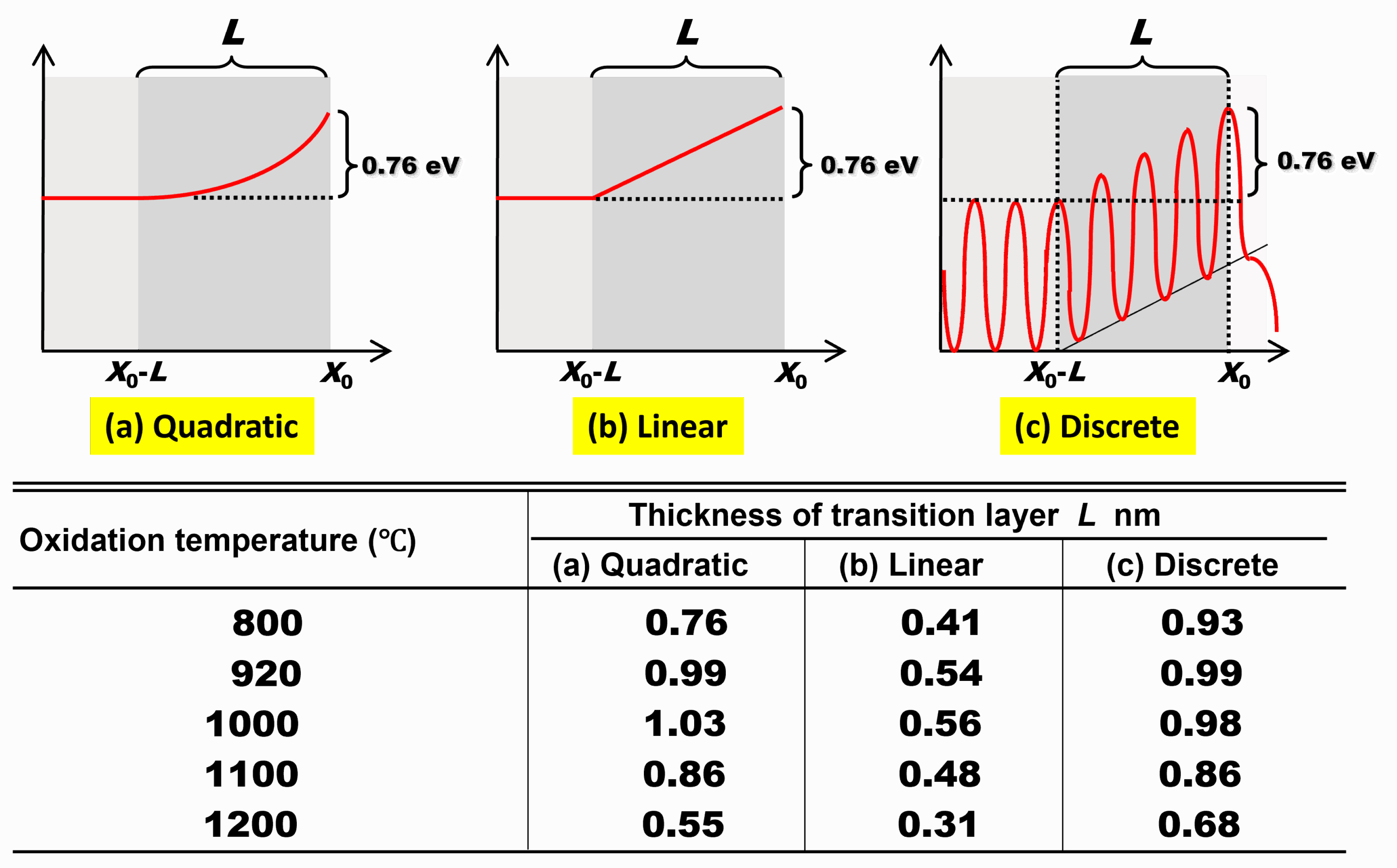
なお、(c)のDiscretizedモデルは、数原子層程度と非常に薄い構造遷移領域をよりリアルに表現するため、離散化した拡散モデルを用いた場合の結果です。導出は複雑になるのでここでは示していませんが、知りたい方は論文[2]をご覧ください。
[1] B. E. Deal, A. S. Grove, J. Appl. Phys. 36, 3770 (1965).
[2] T. Watanabe, K. Tatsumura, I. Ohdomari, Phys. Rev. Lett., 96, 196102 (2006).
完全拡散律速モデル（２）
今回は、Deal-Groveモデルに代わる、完全拡散律速モデルの式を導出します。
酸化膜中の拡散係数は、次式
$$D(x)=\left \{ \begin{array}{ll}D_0,&x<x_0-L\\D_0 \exp \left [ -\frac{\Delta E(x)}{k_BT}\right ],&x\geq x_0-L\end{array}\right .$$
のように、酸化膜中の大部分では\(D(x)=D_0\)で一定とし、界面\(x=x_0\)近傍の厚さ\(L\)の領域で拡散障壁が変化するモデルを仮定します。\(\Delta E(x)\)が、遷移領域内部での拡散障壁の増分を表します。拡散係数\(D\)が深さ依存性を持つように拡張されている点がDeal-Grove方程式との違いです。
酸化膜中の拡散フラックス\(F_2\)は、フィックの法則から濃度勾配と拡散係数の積で与えられます：
$$F_2=-D(x)\frac{d C(x)}{dx}$$
両辺を\(D(x)\)で割って\(x\)について積分すると
$$\int_0^{x_0}F_2\frac{D(x)}dx=-\int_0^{x_0}\frac{dC(x)}{dx}dx$$
$$F_2\int_0^{x_0-L}\frac{1}{D_0}dx+F_2\int_{x_0-L}^{x_0}\frac{1}{D_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx=-\int_{C(0)}^{C(x_0)}dC$$
$$\frac{F_2}{D_0}(x_0-L)+\frac{F_2}{D_0}\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx=C(0)-C(x_0)$$
となります。右辺は、表面のO2濃度\(C(0)=C_0\)と界面のO2濃度\(C(x_0)=C_i\)の差となりますが、完全拡散律速モデルでは界面に到達した酸素は活性化障壁なしで直ちにSiの酸化に消費されるので、\(C(x_0)=C_i=0\)と近似できます。したがって酸化膜中の拡散フラックス\(F_2\)は
$$F_2= \frac{D_0C_0}{x_0-L+L\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx}$$
となります。
あとはDeal-Grove方程式の導出と同じです。
気相から酸化膜表面へのフラックスを\(F_1=h(C^*-C_0)\)とし、ただいま求めた酸化膜中のフラックス\(F_2\)と定常状態で釣り合うとすると、この定常状態のフラックス\(F\)は
$$F= \frac{D_0C^*}{L\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx-L+D_0/h+x_0}$$
となります。これが、界面の単位面積で単位時間に消費される酸化種分子の個数となります。SiO2膜の単位体積当たりに取り込まれる酸化種分子の個数を\(N_1\)とおくと、
$$\frac{dx_0}{dt}=\frac{F}{N_1}=\frac{D_0C^*/N_1}{L\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx-L+D_0/h+x_0}$$
という、SiO2膜厚\(x_0\)の時間に関する新しい微分方程式が得られます。Deal-Grove方程式と同様に
$$\frac{dx_0}{dt}=\frac{B}{A+2x_0}$$
と簡略化して表記すると、\(A\)と\(B\)はそれぞれ
$$A= 2L\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx-2L+2D_0/h$$
$$B = D_0C^*/N_1$$
となります。放物型定数\(B\)はDeal-Gorveモデルの式と全く同じです。一方、定数\(A\)の方はDeal-Groveモデルと異なります。Deal-Grove方程式では界面における酸化反応速度定数に関係しているのに対し、新しい方程式では、構造遷移領域の厚さ\(L\)と構造遷移領域内の拡散障壁の増分\(\Delta E(x)\)に依存する、やや複雑な式に変わっています。
拡散係数もいろいろ(9)
渡邉孝信（早稲田大学・電子物理システム学科）
平均二乗変位と拡散係数の関係
ブラウン運動の理論によると、１次元系の拡散係数\(D\)は
$$\overline{\Delta x^2}=\overline{{(x(t)-x(0))}^2}=2Dt\label{meansquare}\tag{9.1}$$
のように平均二乗変位\(\overline{\Delta x^2}\)に関係づけられます。３次元なら
$$\overline{\Delta r^2}=\overline{{(r(t)-r(0))}^2}=6Dt\tag{9.2}$$
です。
１次元系において、時間\(t\)を\(n\)個の微小時間\(\Delta t_i\) \((i=1,2,⋯,n)\)に区切り、各微小時間における変位を\(l_i\) \((i=1,2,⋯,n)\)とすると、平均二乗変位\(\overline{\Delta x^2}\)は
$$\overline{\Delta x^2}=\left < {\left(\sum_{i=1}^nl_i \right)}^2 \right >=\sum_{i=1}^n\left < {l_i}^2 \right >+2\sum_{i=1}^{n-1}\sum_{j>i}^n\left < l_il_j \right >\tag{9.3}$$
と書けます。ブラウン運動する粒子の異なる時間の変位は無相関であり、
$$\left < l_il_j \right >=0,\;\;\;\;i\neq j\tag{9.4}$$
が成り立つので、式\(\eqref{meansquare}\)は
$$2Dt=\sum_{i=1}^n\left < {l_i}^2 \right >=n\left< {l}^2 \right >\tag{9.5}$$
と書けます。今、議論を簡単にするため、どの微小時間\(\Delta t_i\)も等しく\(\Delta t_i=\Delta t\)と仮定すると
$$n\left< {l}^2 \right >=2nD\Delta t\tag{9.6}$$
となり、拡散係数は
$$D=\frac{\left< {l}^2 \right >}{2\Delta t}\label{diffusivity9}\tag{9.7}$$
と書けることになります。式\(\eqref{diffusivity9}\)において、\(\Delta t\)を平均自由時間\(\overline{t}\)、\(\left< {l}^2 \right >\)を平均自由行程\(\overline{l}\)の二乗とおくと、１次元系の拡散係数は
$$D=\frac{\overline{l}^2}{2\overline{t}}\label{diffusivity9a}\tag{9.8}$$
３次元では
$$D=\frac{\overline{l}^2}{6\overline{t}}\tag{9.9}$$
となり、1/2の係数がかかることになります。
前回までの議論で、せっかく\(D=\overline{l}^2/3\overline{t}\)で話がまとまりそうだったのに、ブラウン運動理論を考えたら、1/2の係数の問題が再燃してしまいました。いったいどう考えればよいのでしょうか？
ここでもやはり、「平均」をどう考えるかが鍵を握っています。式\(\eqref{diffusivity9}\)から式\(\eqref{diffusivity9a}\)に進むとき、\(\left< {l}^2 \right >\)を平均自由行程\(\overline{l}\)の二乗とおいたのですが、この平均操作では、
$$p(l)=\delta(l-\overline{l})\tag{9.10}$$
というデルタ関数分布を暗に仮定していたことになります。この場合、拡散係数は
$$D=\frac{\left< {l}^2 \right >}{2\overline{t}}=\frac{1}{2\overline{t}}\int_0^\infty l^2p(l)dl =\frac{1}{2\overline{t}}\int_0^\infty l^2\delta(l-\overline{l})dl =\frac{\overline{l}^2}{2\overline{t}}\label{diffusivity9b}\tag{9.11}$$
で与えられるのです。ブラウン運動理論では、\(\Delta t\)の間の移動量が\(\overline{l}\)に限定される簡単な酔歩モデルがよく用いられますが、その例では式\(\eqref{diffusivity9b}\)でよいのです。
一方、衝突イベントが定常ポアソン過程となる場合、自由行程の分布は指数分布
$$p(l)=\frac{1}{\overline{l}}e^{-\frac{l}{\overline{l}}}\tag{9.12}$$
となります。この場合は
$$\begin{eqnarray}D&=&\frac{\left< {l}^2 \right >}{2\overline{t}}=\frac{1}{2\overline{t}}\int_0^\infty l^2p(l)dl =\frac{1}{2\overline{t}}\int_0^\infty l^2\frac{1}{\overline{l}}e^{-\frac{l}{\overline{l}}}dl{\overline{t}}\\&=&\frac{1}{2\overline{t}}\cancel{{\left [- l^2 e^{-\frac{l}{\overline{l}}}\right] }_0^\infty}+\frac{1}{2\overline{t}}\int_0^\infty2le^{-\frac{l}{\overline{l}}}dl\\&=&\frac{1}{\overline{t}}\int_0^\infty le^{-\frac{l}{\overline{l}}}dl\\&=&\frac{1}{\overline{t}}\cancel{{\left [- l\overline{l} e^{-\frac{l}{\overline{l}}}\right] }_0^\infty}+\frac{1}{\overline{t}}\int_0^\infty \overline{l}e^{-\frac{l}{\overline{l}}}dl\\&=&\frac{1}{\overline{t}}\int_0^\infty \overline{l}e^{-\frac{l}{\overline{l}}}dl\\&=&\frac{1}{\overline{t}}{\left [- \overline{l}^2 e^{-\frac{l}{\overline{l}}}\right] }_0^\infty=\frac{\overline{l}^2}{\overline{t}}\tag{9.13}\end{eqnarray}$$
となり、1/2の係数が消えます。３次元の場合はもちろん、
$$D=\frac{\overline{l}^2}{3\overline{t}}\tag{9.14}$$
です。
拡散係数もいろいろ(8)
渡邉孝信（早稲田大学・電子物理システム学科）
前回の記事で導出した無衝突で進める確率を用いて、第４回の記事で示した拡散係数を定式化しなおしてみましょう。図8.1に示すように、 \(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。今度は、\(x=x_0\)の面に到達する電子の出発位置を限定せず、距離に応じた到達確率を乗じて全区間で積分することによって、拡散流量を求めます。
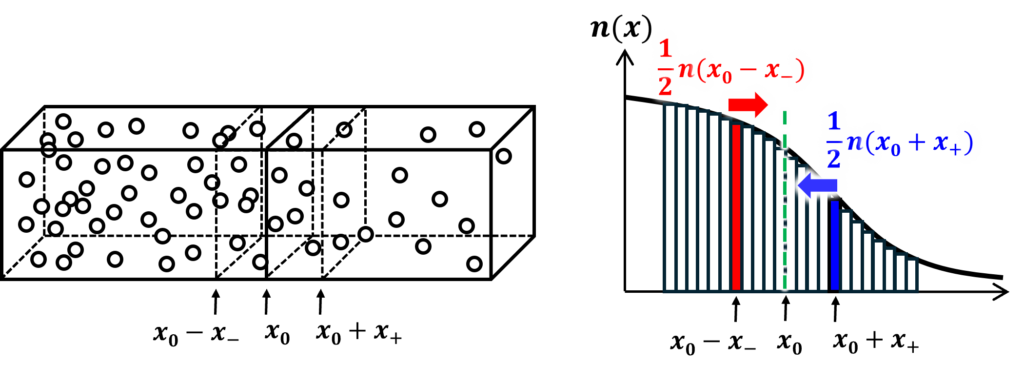
\(x=x_0-x_{-}\)の位置にある電子に注目してみましょう。ここにある電子の1/2が\(+x\)方向を向いているので、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面に到達する可能性がある電子は\(\frac{1}{2}n(x_0-x_{-})dx\)です。これに到達確率\(P_{\rm free}(x_{-})\)を乗じた個数が、無衝突で\(x=x_0\)に到達できます。位置\(x_{-}\)から\(+x\)方向に通過する電子の平均流束を\(f_+(x_{-})dx\)とすると、
$$f_+(x_{-})dx=n(x_0-x_{-})P_{\rm free}(x_{-})\frac{dx}{2\overline{t}}\tag{8.1}$$
と書けます。同様に、位置\(x_{+}\)から\(-x\)方向に通過する電子の平均流束\(f_{-}(x_{+})dx\)は
$$f_-(x_{+})dx=n(x_0+x_{+})P_{\rm free}(x_{+})\frac{dx}{2\overline{t}}\tag{8.2}$$
以上から、\(x=x_0\)における\(+x\)方向への正味の流束\(F_x\)は
$$\begin{eqnarray}F_x &=&\int_0^\infty dx \left \{ f_+(x) – f_{-}(x)\right \}\\&=& \int_0^\infty dxP_{\rm free}(x)\frac{1}{2\overline{t}}\left\{n(x_0-x)-n(x_0+x)\right\}\\&=&-\frac{1}{2\overline{t}}\int_0^\infty dxP_{\rm free}(x)\frac{dn}{dx}\cdot 2x \\&=&-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^\infty x P_{\rm free}(x)dx\label{netflux}\tag{8.3}\end{eqnarray}$$
となります。
ここで、前回求めた到達確率の式
$$P_{\rm free}(x)=e^{-\frac{x}{\overline{l_x}}}\tag{8.4}$$
を式\(\eqref{netflux}\)に代入すると、
$$F_x=-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^\infty x e^{-\frac{x}{\overline{l_x}}}dx=-\frac{\overline{l_x}^2}{\overline{t}}\frac{dn}{dx}=-\overline{v_x}\overline{l_x}\frac{dn}{dx}\tag{8.5}$$
となり、ジィーの本で書かれている拡散係数
$$D=\overline{v_x}\overline{l_x}\tag{8.6}$$
と一致します。３次元なら
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{8.7}$$
です。
あるいはもし、\(P_{\rm free}(x)\)として
$$P_{\rm free}(x)=\left\{\begin{array}{ll}1,&x\leq\overline{l_x}\\0,&x>\overline{l_x}\end{array}\right.\tag{8.8}$$
を仮定すると、
$$F_x=-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^{\overline{l_x}} x dx=-\frac{\overline{l_x}^2}{2\overline{t}}\frac{dn}{dx}=-\frac{\overline{v_x}\overline{l_x}}{2}\frac{dn}{dx}\tag{8.9}$$
となり、アンダーソンらの本の拡散係数と同様、1/2の係数がつくことになります。３次元なら
$$D=\frac{1}{6}\overline{v}\overline{l}\tag{8.10}$$
です。
以上から、ジィーとアンダーソンの拡散係数の違いが、無衝突距離の確率分布の違いで説明できることがわかりました。適切な式はどちらかと言えば、指数関数の到達確率で導かれる
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{8.7 再掲}$$
の方でしょう。
ここまで詳しく見ていくと、\(D=\overline{v}\overline{l}/3\)という拡散係数の式の導き方にも、いろいろツッコミどころが残ることがわかります。
- 無衝突で進んだ電子のみカウントしているが、衝突したら電子が停止してしまうわけでないのだから、複数回散乱して\(x=x_0\)面に到達する確率も考慮すべきではないか。
- そもそも、１回の衝突で過去の運動の履歴が完全に忘却され、次の進行方向が等方的になるという仮定に無理がある。
- 「\(x=x_0-x_{-}\)の位置にある電子のうち、右向きの速度を持つ1/2の電子が\(x=x_0\)面に到達する可能性がある」としているが、ほとんどゼロに近い\(v_x\)を持っている電子も結構あるので、1/2は過大評価ではないか。この傾向は\(x=x_0\)から離れるほど顕著になるはずである。
上記の指摘は至極真っ当で、このような問題点を改善しようとした仕事も過去に行われたようですが、満足のいく定式化には至っていないようです。無理に係数を特定せず、パウリの本やランダウ-リフシッツの本のように、係数に曖昧さを明示的に残しておくことが、最も誠実な書き方と言えるでしょう。
拡散係数もいろいろ(7)
渡邉孝信（早稲田大学・電子物理システム学科）
距離\(r\)まで無衝突で進める確率を定式化する
電子が無衝突で進める距離\(r\)の確率も、指数分布に従うと考えられます。今回は、この確率分布を簡単なモデルを使って導出してみましょう。
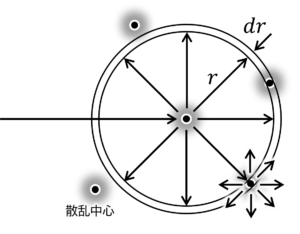
今、ある電子が、最後に衝突イベントを経験してから、距離\(r\)を無衝突で進んだとし、距離\(r\)と\(r+dr\)の間で次の衝突が起こる確率を考えましょう。この散乱は図7.1に示すように等方的で、衝突後に進む方向は球対称となります。電子の散乱を引き起こす散乱中心の個数密度を\(N_s\)、散乱中心の衝突断面積を\(\sigma\)とおくと、半径\(r\)、厚さ\(dr\)の球殻の体積が\(4\pi r^2dr\)であるので、微小区間\(dr\)の衝突確率は
$$\frac{N_s4\pi r^2 dr\sigma}{4\pi r^2}=N_s\sigma dr\tag{7.1}$$
となります。よって、微小距離\(dr\)を無衝突で進める確率は
$$1-N_s\sigma dr \tag{7.2}$$
です。距離\(r\)を無衝突で進む確率\(p_{\rm free}(r)\)と、距離\(r+dr\)を無衝突で進む確率\(p_{\rm free}(r+dr)\)の間には
$$ p_{\rm free}(r+dr) = p_{\rm free}(r)(1-N_s\sigma)dr\tag{7.3}$$
という関係が成り立つことになります。この式から次の微分方程式
$$ \frac{d p_{\rm free}}{dr}=\frac{p_{\rm free}(r+dr) – p_{\rm free}(r)}{dr}=-N_s\sigma p_{\rm free}(r)\tag{7.4}$$
が導かれるので、一般解を求めると
$$p_{\rm free}(r)=C e^{-N_s\sigma r}\tag{7.5}$$
となります。規格化条件
$$\int_0^\infty p_{\rm free}(r)dr=1\tag{7.6}$$
より、
$$p_{\rm free}(r)=N_s\sigma e^{-N_s\sigma r}\tag{7.7}$$
となります。
無衝突で進める距離の平均が平均自由行程\(\overline{l}\)なので、
$$\overline{l}=\int_0^\infty rp_{\rm free}(r)dr=\int_0^\infty rN_s\sigma e^{-N_s\sigma r}dr=\frac{1}{N_s\sigma}\tag{7.8}$$
よって、\(p_{\rm free}(r)\)は
$$p_{\rm free}(r)=\frac{1}{\overline{l}}e^{-\frac{r}{\overline{l}}}\tag{7.9}$$
と表されます。
ここで少し視点を変えて、今\(r=0\)の位置にある電子が、この先\(r\)まで無衝突で進める確率はどのくらいか？、という問題を考えてみましょう。\(p_{\rm free}(r)dr\)は「\(r\)と\(r+dr\)の区間で初めて次の衝突が起こる確率」を表していますから、距離\(r\)進む間のどこかで衝突が起こる確率は、累積確率
$$\int_0^r p_{\rm free}(r^\prime)dr^\prime\tag{7.10}$$
で表されます。ということは、距離\(r\)進む間に衝突が起きない確率を\(P_{\rm free}(r)\)とすると、
$$P_{\rm free}(r)=1-\int_0^r p_{\rm free}(r^\prime)dr^\prime=e^{-\frac{r}{\overline{l}}}\tag{7.11}$$
と表せることになります。
拡散係数もいろいろ(6)
渡邉孝信（早稲田大学・電子物理システム学科）
そもそも「平均」とは何か？
一般に、確率変数\(X\)の期待値\(\left<X\right>\)は
$$\left<X\right>=\int Xp(X)dX\tag{6.1}$$
で計算されます。ここで\(p(X)\)は確率密度関数です。\(p(X)dX\)が、確率変数\(X\)が\(X\)と\(X+dX\)の値を取る確率を表します。
衝突が起きない時間（無衝突時間）が\(t\)秒間続いたあとで、\(t\)から\(t+dt\)の間に衝突が起こる確率を\(p(t)dt\)とすると、平均自由時間\(\left<t\right>\)は
$$\left<t\right>=\int_0^{\infty}tp(t)dt\tag{6.2}$$
で計算されます。もし\(p(t)\)を
$$p(t)=\left\{\begin{array}{ll}\frac{1}{\overline{t}},&t<\overline{t}\\0,&t\geq\overline{t}\end{array}\right.\label{uniform}\tag{6.3}$$
という一様分布（図6.1(a)参照）と仮定するなら、
$$\left<t\right>=\int_0^{\overline{t}}\frac{t}{\overline{t}}dt=\frac{1}{\overline{t}}{\left [\frac{1}{2}t^2 \right ]}_0^{\overline{t}}=\frac{\overline{t}}{2}\label{meanuni}\tag{6.4}$$
となり、ドルーデが最初に定式化したドリフト移動度の式
$$\mu=\frac{q\overline{t}}{2m} （←間違い！）\label{drude}\tag{5.1 再掲}$$
が導かれます。
一方、電子の衝突は全く偶発的に起こるイベントと考えられ、定常ポアソン過程で記述されます。その場合、衝突と衝突の時間間隔が従う分布関数\(p(t)\)は、指数分布
$$p(t)=\frac{1}{\overline{t}}e^{-\frac{t}{\overline{t}}}\label{expdist}\tag{6.5}$$
に従います（図6.1(b)参照）。そうすると、無衝突時間の平均は
$$\left<t\right>=\int_0^{\overline{t}}t\frac{1}{\overline{t}}e^{-\frac{t}{\overline{t}}}dt=\overline{t}\label{meanexp}\tag{6.6}$$
となり、正しいドリフト移動度の式
$$\mu=\frac{q\overline{t}}{m} （←正しい！）\tag{5.5 再掲}$$
が導かれます。
式\(\eqref{uniform}\)の一様分布では、上限の\(\overline{t}\)を超えて無衝突時間が継続することはありませんが、式\(\eqref{expdist}\)では非常に長く無衝突時間が継続することも、低い確率ながら起こりえます。持続時間が長いサンプルは、積分する際に時間が大きな重みとして効いてきますので、発生確率が低くてもそれなりに期待値に寄与するのです。その結果、式\(\eqref{meanexp}\)のように期待値が式\(\eqref{meanuni}\)の２倍になるのです。
このように、一口に「平均」と言っても、どんな確率分布を想定するかによって、その結果は顕著に変わりうるのです。
拡散係数もいろいろ(5)
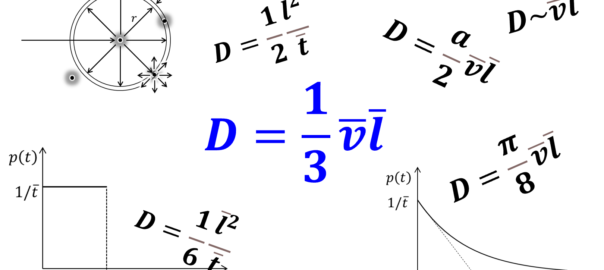
渡邉孝信（早稲田大学・電子物理システム学科）
ドルーデも1/2倍していた！
係数に1/2倍の違いが生じる問題は、第２回で少し触れたように、ドリフト移動度\(\mu\)でも起こっていました。ドルーデが1900年に発表した電気伝導理論の論文で
$$\mu=\frac{q\overline{t}}{2m} （←間違い！）\label{drude}\tag{5.1}$$
と定式化されていたのです。この問題を掘り下げていくと、拡散係数の1/2倍の違いの原因も見えてきます。まず、ドリフト移動度についておさらいをしたのち、どうして移動度を式\(\eqref{drude}\)で表したのか、式\(\eqref{drude}\)がどうして誤りだという結論に至ったのか、見ていくことにしましょう。
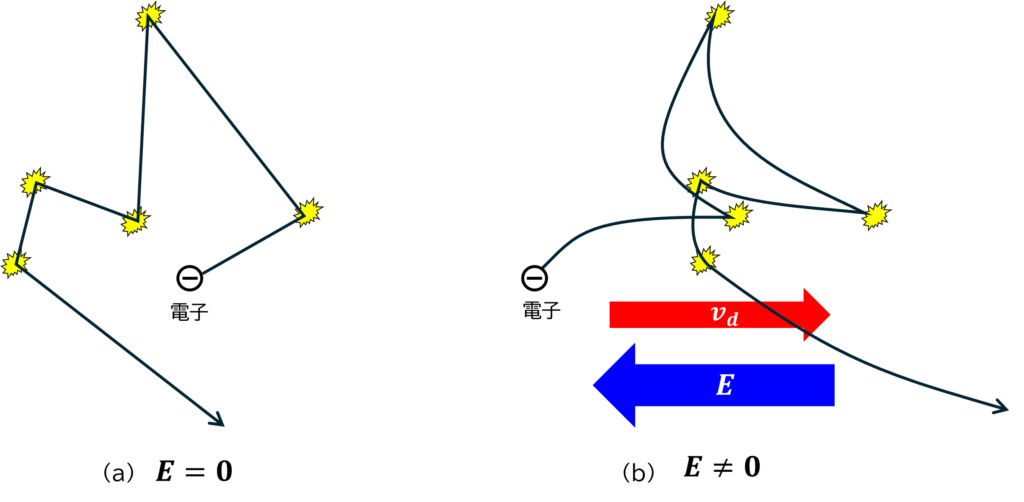
図5.1は、導体中の電子の運動の軌跡を模式的に示した図です。図5.1(a)は外から電界が印加されていない状態です。電子は熱エネルギーをもって絶えずブラウン運動していますが、不純物イオンやフォノンなどと衝突を起こす度に頻繁に移動方向を変え、移動方向は完全にランダムになります。時間平均を取ると特定の方向への移動はなくなり、正味の電流はゼロとなります。
図5.1(b)は、外部から電界を印加したときの様子です。この場合も電子はランダムな運動をしますが、衝突イベントと衝突イベントの間に電界によって加速されます。長時間平均を取ると、電子は定常的な速度\(\boldsymbol{v}_d\)で電界ベクトルの方向（と逆向き）に移動する傾向を示します。 \(\boldsymbol{v}_d\)がドリフト速度です。
電子のドリフト移動度\(\mu\) (cm\({}^2\)・V\({}^{-1}\)s\({}^{-1}\))は、次式で定義されます。
$$\mu\equiv -\frac{\boldsymbol{v}_d}{\boldsymbol{E}}\tag{5.2}$$
\(\boldsymbol{E}\)（V/cm）は外部から印加する電界です。この式、つまりドリフト速度を、平均自由時間\(\overline{t}\)を使った微視的な描像で定式化してみましょう。
今、外部電界\(E\)が\(x\)軸方向に一様に印加されているとし、個々の電子がニュートン方程式に従って運動するとみなすと、運動方程式の\(x\)成分は
$$m\frac{d v_x}{dt}=-qE\tag{5.3}$$
となります。直近の衝突が時刻0で起こったとし、次の衝突が起こる前の時刻を\(t\)とすると、運動方程式の解は
$$m v_x(t)-mv_x(0)=-qEt\tag{5.4}$$
となります。これを多数の電子についてアンサンブル平均をとると、
$$m\left <v_x(t)-v_x(0)\right >=-qE\left<t\right>\tag{5.4}$$
となります。左辺の\(\left <v_x(t)-v_x(0)\right >\)は、衝突と衝突の間に獲得する速度の平均なので、これがドリフト速度 \(v_d\)とみなせます。右辺の\(\left < t\right >\)は、電界によって加速される時間のアンサンブル平均です。これを平均自由時間、すなわち\(\left<t\right>=\overline{t}\)とみなせば、
$$\mu=\frac{q\overline{t}}{m} （←正しい！）\tag{5.5}$$
となり、期待どおりのドリフト移動度の式が導かれます。
一方、ドルーデが最初に示した式\(\eqref{drude}\)では、 \(\left < t \right > =\overline{t}/2\)としていることになります。
どうして1/2倍したくなるのか？
ドルーデが\(\mu=q\overline{t}/(2m)\)を採用する決め手となった理由はおそらく、金属の電気伝導度と熱伝導度の比が温度に比例するというヴィーデマン・フランツ則が、 \(\mu=q\overline{t}/(2m)\)とおくことで、当時の古典論の枠組みで定量的に説明できた（できてしまった）からだと想像できます。しかし、ドルーデほどの人がつじつま合わせをしたわけではないでしょうから、1/2倍した明確な根拠もあったはずです。
ドルーデがどうして\(\mu=q\overline{t}/(2m)\)としたのか、真意はわかりませんが、次のように考えれば、1/2をつけたくなる気持ちが想像できます。
図5.2は、時間間隔\(\overline{t}\)で衝突する典型的な電子が、電界から獲得する速度と時間の関係を示したグラフです。前の衝突から次の衝突までの間、速度は時間に比例して増加します。衝突の度に速度はリセットされ、熱運動以外の速度成分はゼロとなります。すると、平均自由時間\(\overline{t}\)内に電界によって増える速度成分の時間平均は、最終的に獲得する速度\(qE\overline{t}/m\)の1/2となります。
一見まっとうな考え方に思えますが、一体、この考え方のどこが良くないのでしょう？ この疑問は、「平均値」を計算する際に暗に想定している「確率分布」の違いに気づくことで解消できます。
拡散係数もいろいろ(4)
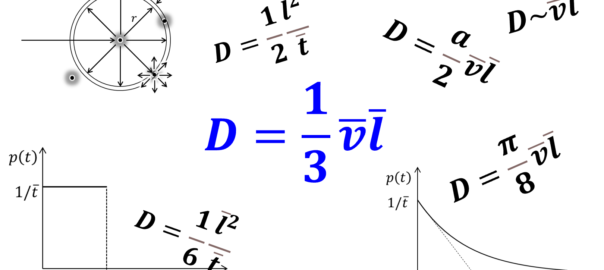
渡邉孝信（早稲田大学・電子物理システム学科）
前々回の記事で、\(D=\overline{v}\overline{l}/3\)であれば、エネルギー等分配則とアインシュタインの関係式を使ってドリフト移動度\(\mu\)と関係づけることができることを示しました。さらに前回の記事で、\(D=\overline{v}\overline{l}/3\)という式は、ボルツマン方程式の定緩和時間近似の解から導かれる拡散係数とも整合する、という話をしました。
しかし、気体分子運動論に基づく初等的な方法で\(D=\overline{v}\overline{l}/3\)を導こうとすると、少々やっかいな問題が起こります。今回はこの問題を掘り下げてみます。
半導体デバイスの代表的テキストと言えば、ジィー（S. M. Sze）の本でしょう。最近ではベティ・アンダーソンとリチャード・アンダーソンの「半導体デバイスの基礎」が現代的テキストとして世界標準になっているようです。ジィーの本は何種類かありますが、気体分子運動論を用いて拡散係数\(D\)を導いているのは、初学者向けの「半導体デバイス：基礎理論とプロセス技術」です。まずは、このジィーの説明を見ていきましょう。
ジィーの本の説明
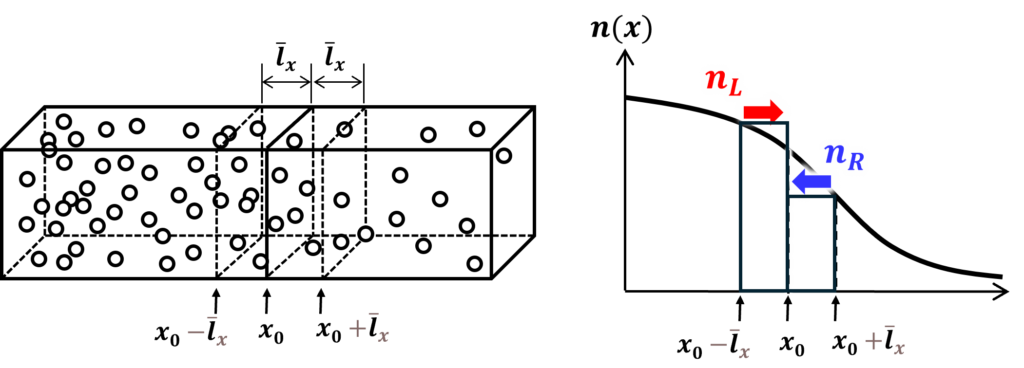
図4.1に示すように、\(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。\(x=x_0\)の面を、単位時間、単位面積あたりに通過する電子の数を計算してみましょう。電子は平均熱速度\(\overline{v_x}\)で\(x\)軸に沿ってランダムに運動しているものとし、その平均自由行程を\(\overline{l_x}\)とします。平均自由時間を\(\overline{t}\)とすると、\(\overline{l_x}=\overline{v_x}\overline{t}\)が成り立ちます。\(x=x_0-\overline{l_x}\)の位置にある電子の1/2が、\(+x\)方向を向いているので、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面を通過するチャンスがあります。したがって、単位時間、単位面積あたりに\(x=x_0\)の面を、\(+x\)方向に横切る電子の平均流束\(F_+\)は
$$F_+ = \frac{\frac{1}{2}n(x_0-\overline{l_x})\cdot\overline{l_x}}{\overline{t}}=\frac{1}{2}n(x_0-\overline{l_x})\overline{v_x}\label{rightflux}\tag{4.1}$$
とジィーの本で表されています。
同様に、\(x=x_0+\overline{l_x}\)の位置にある電子の1/2が、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面を\(-x\)方向に通過できると考えられるので、単位時間、単位面積あたりに\(x=x_0\)の面を、\(-x\)方向に横切る電子の平均流束\(F_-\)は
$$F_- = \frac{\frac{1}{2}n(x_0+\overline{l_x})\cdot\overline{l_x}}{\overline{t}}=\frac{1}{2}n(x_0+\overline{l_x})\overline{v_x}\label{leftflux}\tag{4.2}$$
となります。
したがって、正味の流束\(F_x\)は
$$F_x=F_+-F_-=\frac{1}{2}\overline{v_x}\left\{ n(x_0-\overline{l_x})-n(x_0+\overline{l_x})\right\}\tag{4.3}$$
となります。ここで、電子密度\(n(x_0\pm \overline{l_x})\)を\(x=x_0\)の周りで1次の項までテーラー展開すると、
$$\begin{eqnarray}F_x &=& \frac{1}{2}\overline{v_x}\left\{n(x_0)-\overline{l_x}\frac{dn}{dx}-n(x_0)-\overline{l_x}\frac{dn}{dx}\right\}\\&=&\frac{1}{2}\overline{v_x}\left(-2\overline{l_x}\frac{dn}{dx} \right)=-\overline{v_x}\overline{l_x}\frac{dn}{dx}\end{eqnarray}\tag{4.4}$$
となり、拡散係数\(D\)は
$$D=\overline{v_x}\overline{l_x}\tag{4.5}$$
となります。３次元空間での平均速度\(\overline{v}=\sqrt{3}\overline{v_x}\)と平均自由行程\(\overline{l}=\sqrt{3}\overline{l_x}\) を使って表すと
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{4.6}$$
となり、ボルツマン方程式から導かれる拡散係数と一致します。
以上の導出は、一見何も問題がなさそうに思えるかもしれません。筆者も学生時代は全く疑問に思いませんでした（たいして深く考えていなかっただけですが）。拡散現象の本質はしっかり捉えているので、これで納得できるならそれで良いのです。
しかし、読者の中には、式\(\eqref{rightflux}\)と式\(\eqref{leftflux}\)において、\(x=x_0\)の面を通過するチャンスがある電子数を
$$\frac{1}{2}n(x_0\pm\overline{l_x})\cdot\overline{l_x}\tag{4.7}$$
とおいている点に違和感を抱く方もいることでしょう。\(x=x_0\)の面を通過できる電子が、\(x_0-\overline{l_x}<x<x_0\)もしくは\(x_0<x<x_0+\overline{l_x}\)の範囲にいる電子（の半数）だとするなら、これらの区間の電子密度を\(x=x_0\pm\overline{l_x}\)の点の密度で代表させてよいものか、と思う方もいるのではないでしょうか。むしろ、\(x=x_0\pm\overline{l_x}/2\)の点の密度で代表させた方がよさそうに思えます。
アンダーソンらの本の説明
ジィーの導出で抱く上記の疑問点を解消したような説明をしているのが、アンダーソンらの「半導体デバイスの基礎」です。この本は第１版が2005年に出版され、樺沢宇紀氏による日本語訳が2008年にシュプリンガージャパンから出版された本です。筆者も2009年から所属学科で開講した「電子デバイス」の教科書として採用し、現在も使用しています。
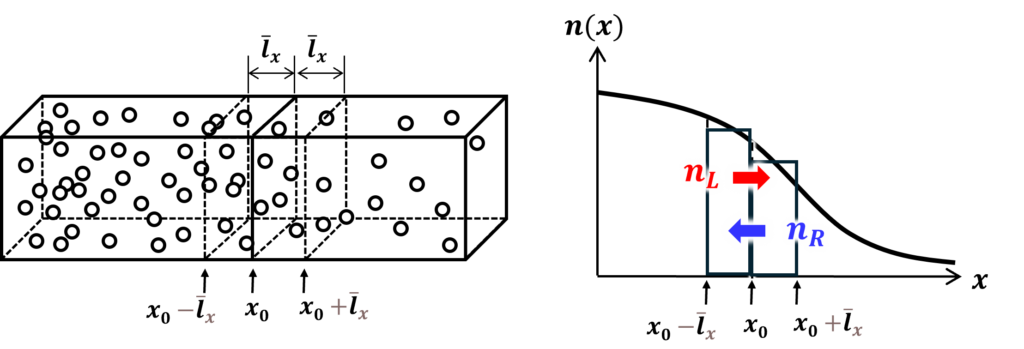
以下の説明はアンダーソンらの本の表現と若干異なりますが、本質的な意味は同じです。考える系もジィーと同じで、図4.2に示すように、\(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。\(x=x_0\)の面を、\(+x\)方向に通過する電子の数は、\(x_0-\overline{l_x}<x<x_0\)の範囲にいる電子の1/2と考えられるので、単位時間、単位面積あたりに\(x=x_0\)の面を、\(+x\)方向に横切る電子の平均流束\(F_+\)は
$$F_+ =\frac{1}{2}n(x_0-\overline{l_x}/2)\overline{v_x}\tag{4.8}$$
となります。同様に\(x=x_0\)の面を、\(-x\)方向に横切る電子の平均流束\(F_-\)は
$$F_- =\frac{1}{2}n(x_0+\overline{l_x}/2)\overline{v_x}\tag{4.9}$$
となります。したがって、正味の流束\(F_+\)は
$$F_x=F_+-F_-=\frac{1}{2}\overline{v_x}\left\{ n(x_0-\overline{l_x}/2)-n(x_0+\overline{l_x}/2)\right\}\tag{4.9}$$
となります。電子密度を\(x=x_0\)の周りで１次の項までテーラー展開すると、
$$\begin{eqnarray}F_x &=& \frac{1}{2}\overline{v_x}\left\{n(x_0)-\frac{\overline{l_x}}{2}\frac{dn}{dx}-n(x_0)-\frac{\overline{l_x}}{2}\frac{dn}{dx}\right\}\\&=&-\overline{v_x}\frac{\overline{l_x}}{2}\frac{dn}{dx}\end{eqnarray}\tag{4.10}$$
となり、拡散係数\(D\)は
$$D=\frac{\overline{v_x}\overline{l_x}}{2}\label{andersonsdiffusivity}\tag{4.11}$$
となります。予想できていた方も多いと思いますが、ジィーの本の拡散係数の半分になってしまいました。３次元空間での平均速度\(\overline{v}=\sqrt{3}\overline{v_x}\)と平均自由行程\(\overline{l}=\sqrt{3}\overline{l_x}\) を使って表すと
$$D=\frac{1}{6}\overline{v}\overline{l}\tag{4.12}$$
となります。
アンダーソンらの本の日本語訳版には、訳者の樺沢氏が以下の訳注をつけています。
モデルの設定方法や\(\overline{l}\)、\(\overline{t}\)の定義の仕方に依存して\(D=(1/2)\overline{l}^2/\overline{t}\)の定数項の付き方は微妙に違ってくるので（たとえば３次元系のBoltzmann輸送方程式に基づき緩和時間\(\tau\)の定数近似を採用すると、\(D=(1/3)l^2/\tau\)）、\(D=(1/2)\overline{l}^2/\overline{t}\)を厳密な”定義式”として計算に用いることはないと見てよい。
\(\overline{l}\)、\(\overline{t}\)の定義に依存するとはどういう事なのでしょうか？ 「微妙に違ってくる」とはどういう事なのでしょうか？ 次回以降の記事で、この疑問に答えていきます。
