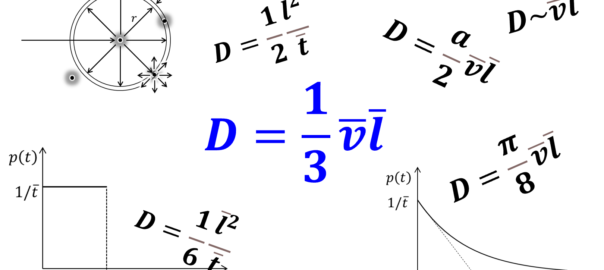渡邉孝信(早稲田大学・電子物理システム学科)
前々回の記事で、\(D=\overline{v}\overline{l}/3\)であれば、エネルギー等分配則とアインシュタインの関係式を使ってドリフト移動度\(\mu\)と関係づけることができることを示しました。さらに前回の記事で、\(D=\overline{v}\overline{l}/3\)という式は、ボルツマン方程式の定緩和時間近似の解から導かれる拡散係数とも整合する、という話をしました。
しかし、気体分子運動論に基づく初等的な方法で\(D=\overline{v}\overline{l}/3\)を導こうとすると、少々やっかいな問題が起こります。今回はこの問題を掘り下げてみます。
半導体デバイスの代表的テキストと言えば、ジィー(S. M. Sze)の本でしょう。最近ではベティ・アンダーソンとリチャード・アンダーソンの「半導体デバイスの基礎」が現代的テキストとして世界標準になっているようです。ジィーの本は何種類かありますが、気体分子運動論を用いて拡散係数\(D\)を導いているのは、初学者向けの「半導体デバイス:基礎理論とプロセス技術」です。まずは、このジィーの説明を見ていきましょう。
ジィーの本の説明
図4.1に示すように、\(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。\(x=x_0\)の面を、単位時間、単位面積あたりに通過する電子の数を計算してみましょう。電子は平均熱速度\(\overline{v_x}\)で\(x\)軸に沿ってランダムに運動しているものとし、その平均自由行程を\(\overline{l_x}\)とします。平均自由時間を\(\overline{t}\)とすると、\(\overline{l_x}=\overline{v_x}\overline{t}\)が成り立ちます。\(x=x_0-\overline{l_x}\)の位置にある電子の1/2が、\(+x\)方向を向いているので、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面を通過するチャンスがあります。したがって、単位時間、単位面積あたりに\(x=x_0\)の面を、\(+x\)方向に横切る電子の平均流束\(F_+\)は
$$F_+ = \frac{\frac{1}{2}n(x_0-\overline{l_x})\cdot\overline{l_x}}{\overline{t}}=\frac{1}{2}n(x_0-\overline{l_x})\overline{v_x}\label{rightflux}\tag{4.1}$$
とジィーの本で表されています。
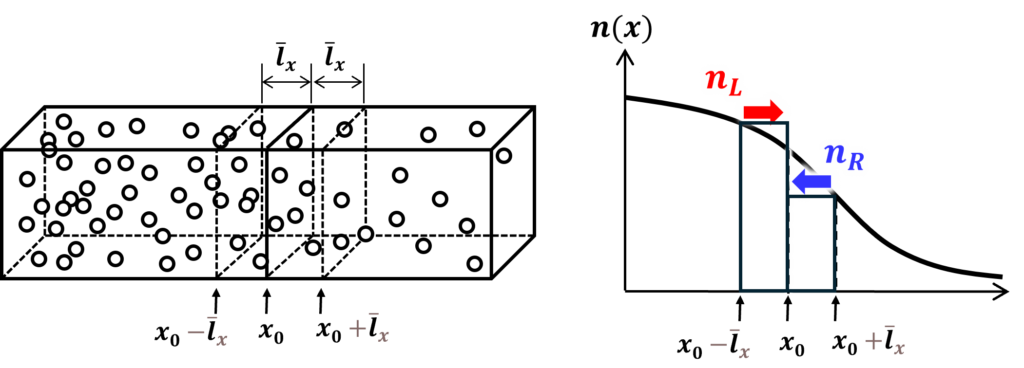
同様に、\(x=x_0+\overline{l_x}\)の位置にある電子の1/2が、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面を\(-x\)方向に通過できると考えられるので、単位時間、単位面積あたりに\(x=x_0\)の面を、\(-x\)方向に横切る電子の平均流束\(F_-\)は
$$F_- = \frac{\frac{1}{2}n(x_0+\overline{l_x})\cdot\overline{l_x}}{\overline{t}}=\frac{1}{2}n(x_0+\overline{l_x})\overline{v_x}\label{leftflux}\tag{4.2}$$
となります。
したがって、正味の流束\(F_x\)は
$$F_x=F_+-F_-=\frac{1}{2}\overline{v_x}\left\{ n(x_0-\overline{l_x})-n(x_0+\overline{l_x})\right\}\tag{4.3}$$
となります。ここで、電子密度\(n(x_0\pm \overline{l_x})\)を\(x=x_0\)の周りで1次の項までテーラー展開すると、
$$\begin{eqnarray}F_x &=& \frac{1}{2}\overline{v_x}\left\{n(x_0)-\overline{l_x}\frac{dn}{dx}-n(x_0)-\overline{l_x}\frac{dn}{dx}\right\}\\&=&\frac{1}{2}\overline{v_x}\left(-2\overline{l_x}\frac{dn}{dx} \right)=-\overline{v_x}\overline{l_x}\frac{dn}{dx}\end{eqnarray}\tag{4.4}$$
となり、拡散係数\(D\)は
$$D=\overline{v_x}\overline{l_x}\tag{4.5}$$
となります。3次元空間での平均速度\(\overline{v}=\sqrt{3}\overline{v_x}\)と平均自由行程\(\overline{l}=\sqrt{3}\overline{l_x}\) を使って表すと
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{4.6}$$
となり、ボルツマン方程式から導かれる拡散係数と一致します。
以上の導出は、一見何も問題がなさそうに思えるかもしれません。筆者も学生時代は全く疑問に思いませんでした(たいして深く考えていなかっただけですが)。拡散現象の本質はしっかり捉えているので、これで納得できるならそれで良いのです。
しかし、読者の中には、式\(\eqref{rightflux}\)と式\(\eqref{leftflux}\)において、\(x=x_0\)の面を通過するチャンスがある電子数を
$$\frac{1}{2}n(x_0\pm\overline{l_x})\cdot\overline{l_x}\tag{4.7}$$
とおいている点に違和感を抱く方もいることでしょう。\(x=x_0\)の面を通過できる電子が、\(x_0-\overline{l_x}<x<x_0\)もしくは\(x_0<x<x_0+\overline{l_x}\)の範囲にいる電子(の半数)だとするなら、これらの区間の電子密度を\(x=x_0\pm\overline{l_x}\)の点の密度で代表させてよいものか、と思う方もいるのではないでしょうか。むしろ、\(x=x_0\pm\overline{l_x}/2\)の点の密度で代表させた方がよさそうに思えます。
アンダーソンらの本の説明
ジィーの導出で抱く上記の疑問点を解消したような説明をしているのが、アンダーソンらの「半導体デバイスの基礎」です。この本は第1版が2005年に出版され、樺沢宇紀氏による日本語訳が2008年にシュプリンガージャパンから出版された本です。筆者も2009年から所属学科で開講した「電子デバイス」の教科書として採用し、現在も使用しています。
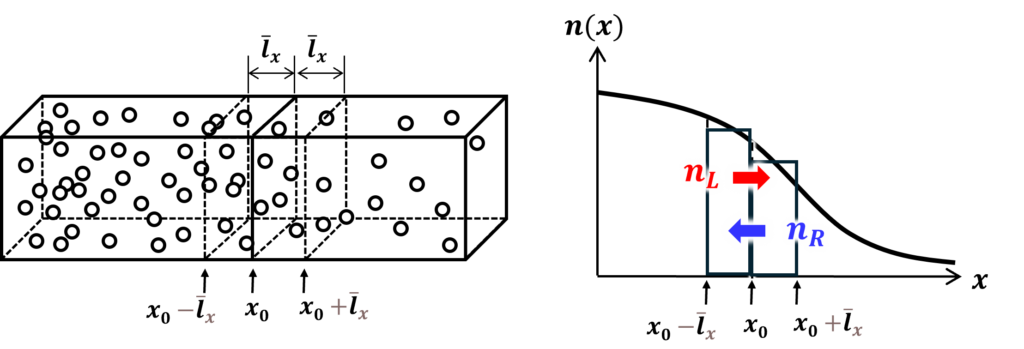
以下の説明はアンダーソンらの本の表現と若干異なりますが、本質的な意味は同じです。考える系もジィーと同じで、図4.2に示すように、\(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。\(x=x_0\)の面を、\(+x\)方向に通過する電子の数は、\(x_0-\overline{l_x}<x<x_0\)の範囲にいる電子の1/2と考えられるので、単位時間、単位面積あたりに\(x=x_0\)の面を、\(+x\)方向に横切る電子の平均流束\(F_+\)は
$$F_+ =\frac{1}{2}n(x_0-\overline{l_x}/2)\overline{v_x}\tag{4.8}$$
となります。同様に\(x=x_0\)の面を、\(-x\)方向に横切る電子の平均流束\(F_-\)は
$$F_- =\frac{1}{2}n(x_0+\overline{l_x}/2)\overline{v_x}\tag{4.9}$$
となります。したがって、正味の流束\(F_+\)は
$$F_x=F_+-F_-=\frac{1}{2}\overline{v_x}\left\{ n(x_0-\overline{l_x}/2)-n(x_0+\overline{l_x}/2)\right\}\tag{4.9}$$
となります。電子密度を\(x=x_0\)の周りで1次の項までテーラー展開すると、
$$\begin{eqnarray}F_x &=& \frac{1}{2}\overline{v_x}\left\{n(x_0)-\frac{\overline{l_x}}{2}\frac{dn}{dx}-n(x_0)-\frac{\overline{l_x}}{2}\frac{dn}{dx}\right\}\\&=&-\overline{v_x}\frac{\overline{l_x}}{2}\frac{dn}{dx}\end{eqnarray}\tag{4.10}$$
となり、拡散係数\(D\)は
$$D=\frac{\overline{v_x}\overline{l_x}}{2}\label{andersonsdiffusivity}\tag{4.11}$$
となります。予想できていた方も多いと思いますが、ジィーの本の拡散係数の半分になってしまいました。3次元空間での平均速度\(\overline{v}=\sqrt{3}\overline{v_x}\)と平均自由行程\(\overline{l}=\sqrt{3}\overline{l_x}\) を使って表すと
$$D=\frac{1}{6}\overline{v}\overline{l}\tag{4.12}$$
となります。
アンダーソンらの本の日本語訳版には、訳者の樺沢氏が以下の訳注をつけています。
モデルの設定方法や\(\overline{l}\)、\(\overline{t}\)の定義の仕方に依存して\(D=(1/2)\overline{l}^2/\overline{t}\)の定数項の付き方は微妙に違ってくるので(たとえば3次元系のBoltzmann輸送方程式に基づき緩和時間\(\tau\)の定数近似を採用すると、\(D=(1/3)l^2/\tau\))、\(D=(1/2)\overline{l}^2/\overline{t}\)を厳密な”定義式”として計算に用いることはないと見てよい。
\(\overline{l}\)、\(\overline{t}\)の定義に依存するとはどういう事なのでしょうか? 「微妙に違ってくる」とはどういう事なのでしょうか? 次回以降の記事で、この疑問に答えていきます。