Deal-Groveの微分方程式
$$ \frac{dx_0}{dt}=\frac{B}{A+2x_0}$$
の解を求めてみましょう。これは変数分離法で解ける簡単な問題です。
$$ (A+2x_0) dx_0=B dt$$
として両辺を不定積分し、一般解を求めます。
$$\int^{x_0}(A+2x_0^\prime) dx_0^\prime=\int^tB dt^\prime+C$$
$$\rightarrow\;\;\; x_0^2+Ax_0 =B t+C$$
\(C\)は未定の積分定数で、これを決定するには境界条件を与える必要があります。境界条件として
$$x_0(0)=x_i$$
を与えましょう。すなわち、時刻\(t=0\)で厚さ\(x_i\)のSiO2膜が既にある、とします。すると、
$$C= x_i^2+Ax_i $$
となり、微分方程式の特解として
$$x_0^2+Ax_0 =B t+ x_i^2+Ax_i $$
が得られます。あるいは、
$$x_0^2+Ax_0 =B (t+\tau) $$
と書いてもよいでしょう。ここで\(\tau=( x_i^2+Ax_i)/B\)はSiO2膜の厚さがちょうどゼロとなる、時間軸との切片(にマイナスの符号をつけた値)に相当します。時間軸\(t\)を\(t+\tau=t^\prime\)とシフトしてあげれば、\(t^\prime=0\)で\(x_0=0\)から始まるスッキリした関係になります。
線形領域と放物型領域
Deal-Grove方程式の解
$$x_0^2+Ax_0 =B (t+\tau) $$
は、線形-放物型方程式と呼ばれます。SiO2膜が薄い初期段階では、\(x_0^2\)が小さく無視できますので、
$$x_0 \simeq \frac{B}{A} (t+\tau) $$
となります。SiO2膜厚\(x_0\)は時間に比例して増加することになります。この近似が成り立つ領域を線形領域(linear region)と呼び、比例係数\(B/A\)は、線形速度定数(linear rate constant)と呼ばれます。
一方、SiO2膜厚\(x_0\)が十分厚くなってくると、\(x_0^2\)に比べて\(Ax_0\)の項が無視できますので、
$$x_0^2 \simeq B (t+\tau) $$
となります。SiO2膜厚\(x_0\)の2乗が時間に比例することになります。この近似が成り立つ領域を放物型領域(parabolic region)と呼び、比例係数\(B\)は、放物型速度定数(parabolic rate constant)と呼ばれます。
SiO2膜厚\(x_0\)の大小によって近似せず、\(x_0\)を一般的な形で表すと、\(x_0>0\)より
$$x_0 =\frac{-A+\sqrt{A^2+4B(t+\tau)}}{2} $$
となります。ここで
$$\frac{x_0}{A/2} =-1+\sqrt{1+\frac{t+\tau}{A^2/4B}} $$
と書き直し、
$$\chi\equiv \frac{x_0}{A/2}$$
$$\theta\equiv \frac{t+\tau}{A^2/4B}$$
と変数変換すると、\(\chi\)と\(\theta\)は
$$\chi =-1+\sqrt{1+\theta} $$
というユニバーサルな関係で表されることになります。
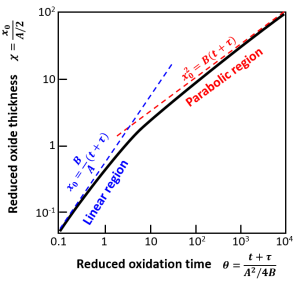
実際、パラメータ\(A\)、\(B\)、\(\tau\)を適切に選ぶと、O2分子を酸化種とする乾燥雰囲気中の酸化(ドライ酸化)でも、H2O分子を酸化種とする水蒸気中の酸化(ウェット酸化)でも、SiO2膜厚\(x_0\)と時間\(t\)の関係を幅広い温度領域で再現することが確認されています。
逆に、線形領域から放物型領域まで、SiO2膜厚\(x_0\)と時間\(t\)の関係を実験で計測して、パラメータ\(A\)、\(B\)、\(\tau\)を抽出してあげれば、その温度依存性などを調べることで、酸化プロセスの素過程に関する多くの手掛かりを得ることができます。