渡邉孝信(早稲田大学・電子物理システム学科)
ド・ブロイが物質波理論を作り上げる過程で目標にしたのが、ボーアの水素原子模型で仮定された量子条件を、粒子に付随する振動の位相一致条件で説明することでした。
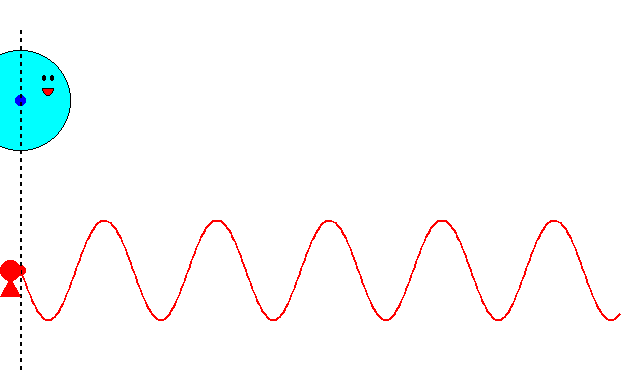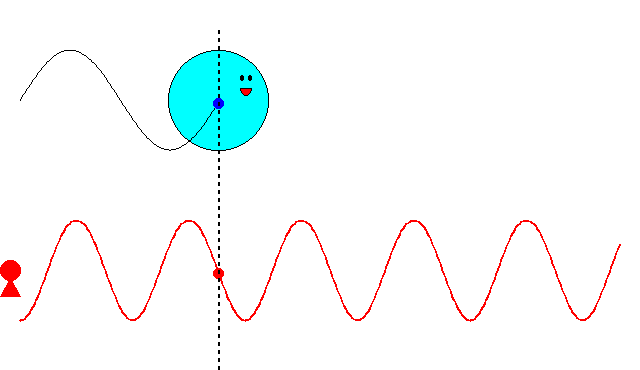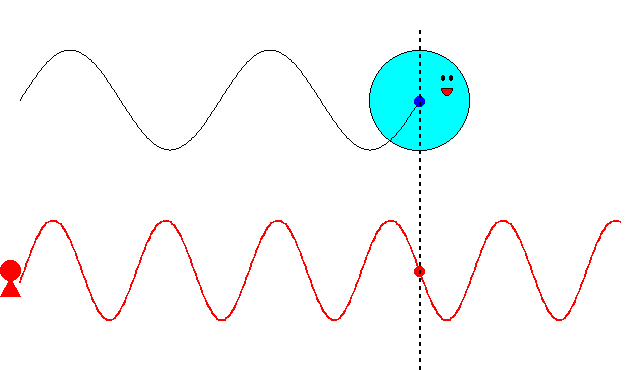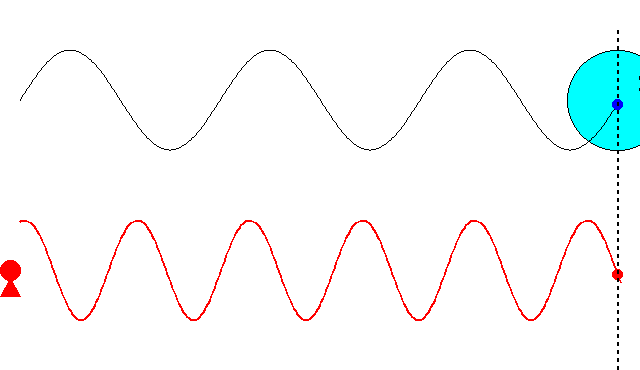
これまでの記事で述べたように、最初ド・ブロイは、\(\nu=mc^2/h\)という振動数の振動現象が、「粒子の内部で」何らかの形で起こっていると考えていました。そして、この振動現象の位相が、原子核の周りを一周するごとに整数の周期分だけ変化すると想定しました。さもなければ、その軌道は不安定になるだろうと考えたからです。しかし、この考え方ではボーアの量子条件を導くことができませんでした。
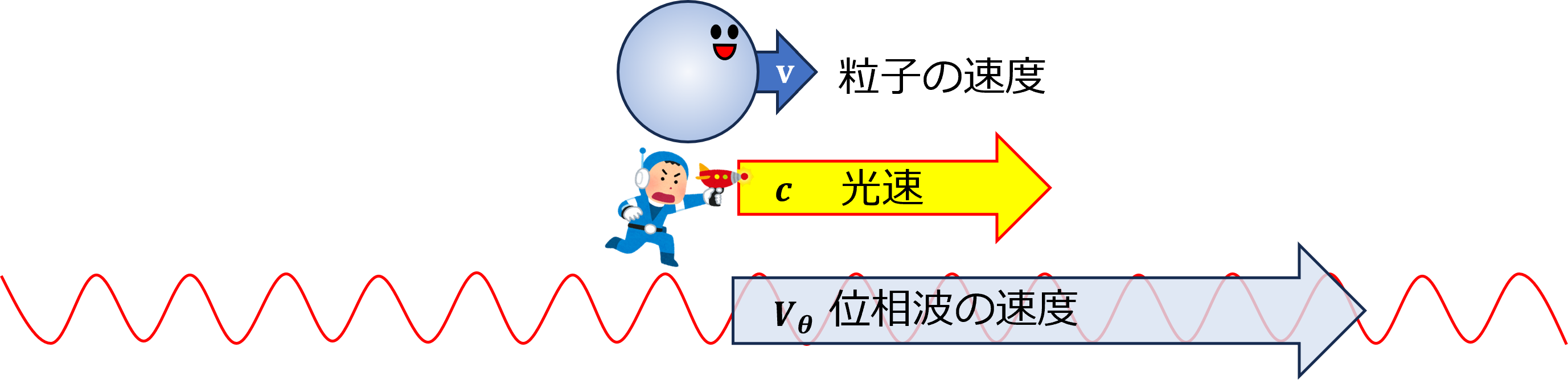
その後、粒子の周囲の空間に広がる、光よりも速いスピードで粒子を先導する位相波という着想に至りました。この位相波が原子核の周りを一周するごとに整数の周期分だけ変化すると考えてみたところ、今度は見事、ボーアの量子条件を導くことに成功しました。これによりド・ブロイは、自身の物質波理論に確固たる自信をもったそうです。
今回の記事では、ド・ブロイがボーアの量子条件を導けるようになるまでの経緯を追ってみたいと思います。
ボーアの水素原子モデル
1913年に発表されたボーアの水素原子モデルでは、電子は原子核のまわりを円軌道に沿って周回すると考えます。電子の軌道が安定であるためには、電子が原子核から受けるクーロン力と、電子の周回運動による遠心力とが釣り合っていなければならないので
$$\frac{mv^2}{r}=\frac{q^2}{4\pi\varepsilon_0 r^2}\label{balance}\tag{6.1}$$
が成り立つ、とします。
ボーアはさらに、「安定状態にある原子では、周回軌道に沿った電子の角運動量の積分がプランク定数\(h\)の整数倍になる」と仮定しました。すなわち
$$\oint P_\theta d\theta = \int_0^{2\pi}mvrd\theta = 2\pi mvr = nh\label{bohr}\tag{6.2}$$
と仮定したのです。右辺の\(n\)は正の整数です。この制約条件のおかげで、電子が取り得る軌道半径\(r\)とエネルギー\(E\)が、とびとびの離散的な値に限定されます。式(\ref{bohr})をボーアの量子条件と呼びます。
 式(\ref{balance})と式(\ref{bohr})から、軌道半径\(r\)とエネルギー\(E\)(運動エネルギーとクーロンポテンシャルの和)は、正の整数\(n\)をパラメータとして
式(\ref{balance})と式(\ref{bohr})から、軌道半径\(r\)とエネルギー\(E\)(運動エネルギーとクーロンポテンシャルの和)は、正の整数\(n\)をパラメータとして
$$r_n = \frac{\varepsilon_0 n^2 h^2}{\pi m q^2}\tag{6.3}$$
$$E_n = -\frac{mq^4}{8 \varepsilon_0^2 n^2 h^2}\label{Henergy}\tag{6.4}$$
と導かれます(クーロンポテンシャルは\(r\rightarrow\infty\)の極限でゼロとしています)。最も低い\(n=1\)の基底状態の半径は\(r_1=0.0529177\) nmで、ボーア半径と呼ばれます。基底エネルギーは\(E_1=-13.6057\) eVで、水素原子のイオン化エネルギーと一致します。
高いエネルギー状態\(E_n\)から低い\(E_{n^\prime}\)に遷移する際(\(n>n^\prime\))に光が放出されますが、この光の振動数\(\nu\)が、アインシュタインの光量子仮説\(E=h\nu\)より
$$E_n-E_{n^\prime}=h\nu \label{enen}\tag{6.5}$$
を満たす振動数に限定されるとすると、水素放電管で観察されるスペクトル線の波長を決める式「リュードベリの公式」を見事に説明できたのです。リュードベリの公式は
$$\frac{1}{\lambda}=R_{\infty}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)\;\;\;\;(n>n^\prime)\tag{6.6}$$
で与えられます。\(R_\infty\)はリュードベリ定数で、実験で\(1.0973\times10^7{\rm m}^{-1}\)と測定されていました。
式(\ref{enen})にエネルギー準位の式(\ref{Henergy})を代入すると、
$$\begin{eqnarray}E_n-E_{n^\prime} &=& -\frac{mq^4}{8 \varepsilon_0^2 n^2 h^2}+\frac{mq^4}{8 \varepsilon_0^2 {n^\prime}^2 h^2}\\ &=&\frac{mq^4}{8\varepsilon_0 h^2}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)=h\nu\end{eqnarray}$$
となります。\(c=\lambda\nu\)より、
$$\frac{1}{\lambda}=\frac{\nu}{c}=\frac{mq^4}{8\varepsilon_0 h^3c}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)\;\;\;\;(n>n^\prime)\tag{6.7}$$
が得られます。\(\frac{mq^4}{8\varepsilon_0 h^3c}\)の数値は\(1.09737315\times10^7{\rm m}^{-1}\)となり、リュードベリ定数の実験値と一致します。
位相一致条件からボーアの量子条件を導く
ボーアの水素原子モデルの成功のカギは、ボーアが仮定した量子条件の式(\ref{bohr})
$$ 2\pi mvr = nh\tag{6.2 再掲}$$
にあります。ド・ブロイは、粒子に付随する振動の位相が、原子核の周りを一周するごとに整数の周期分だけ変化するという条件で、式(\ref{bohr})を導こうとしたのです。
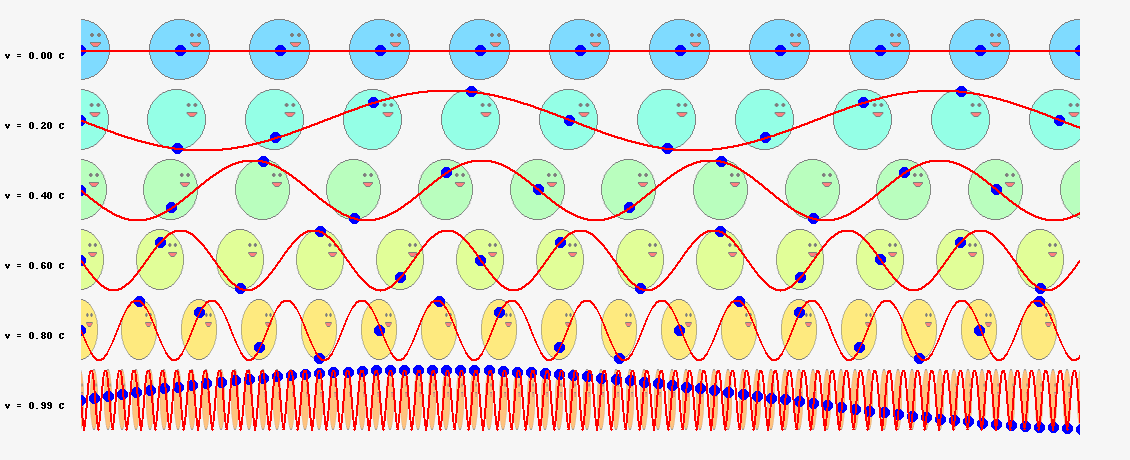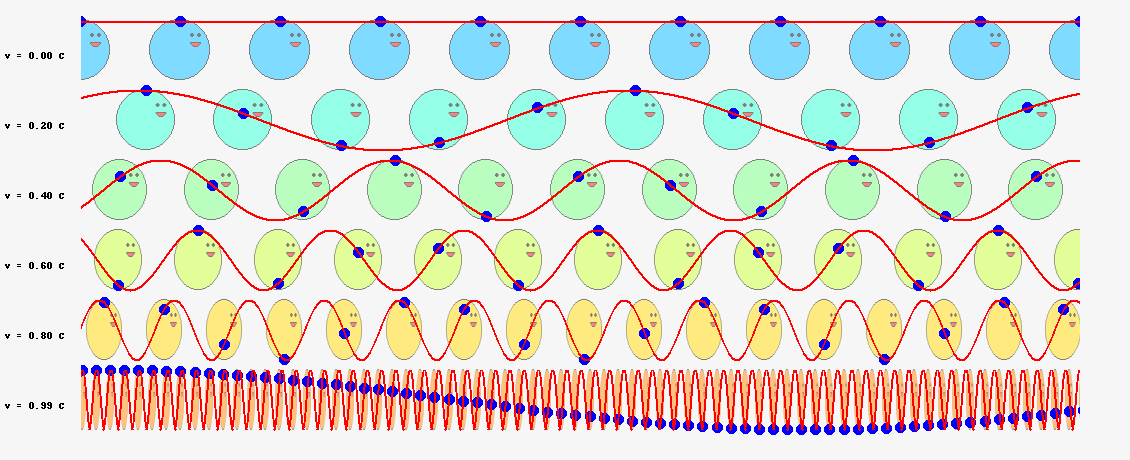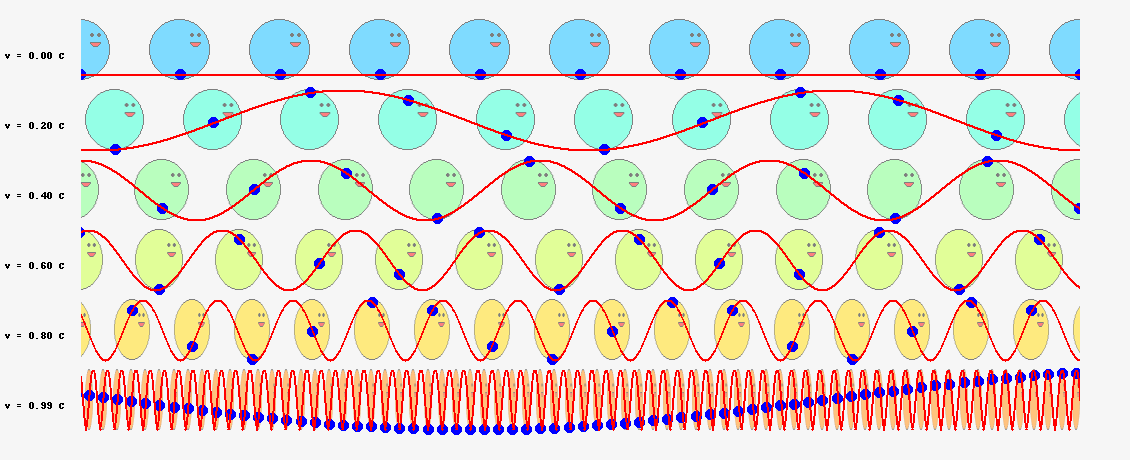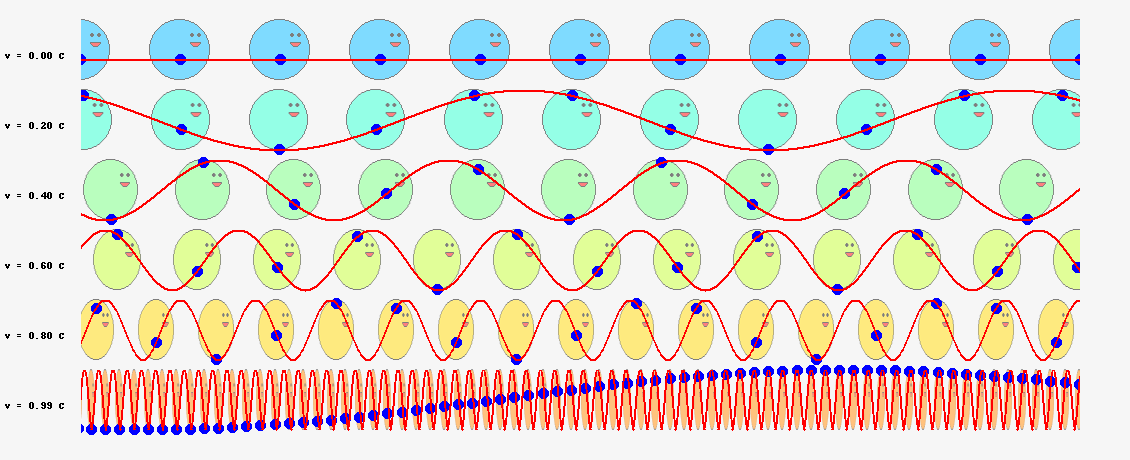
ド・ブロイは当初、\(\nu=mc^2/h\)という振動数の振動現象が、電子の内部で起こっていると考えていました。電子の速度が\(v\)のとき、半径\(r\)の軌道を一周する所要時間は
$$t=\frac{2\pi r}{v}\tag{6.8}$$
ですから、軌道を一周する間に進む位相は
$$2\pi \nu t=2\pi \frac{2\pi mc^2}{vh}\tag{6.9}$$
となります。これが\(2\pi\)の整数倍に限定されるとすると
$$2\pi \frac{2\pi mc^2}{vh}=2\pi n\;\;\;\;(残念、失敗!)\tag{6.10}$$
という量子条件が導かれます。残念ながら、ボーアの量子条件の式(\ref{bohr})と一致しません。ここでは\(v\)は光速\(c\)より十分小さいとし、振動数にローレンツ因子はかけませんでしたが、たとえかけたとしてもボーアの量子条件にはなりません(円運動なのでそもそも特殊相対論の範疇を超えていますが)。
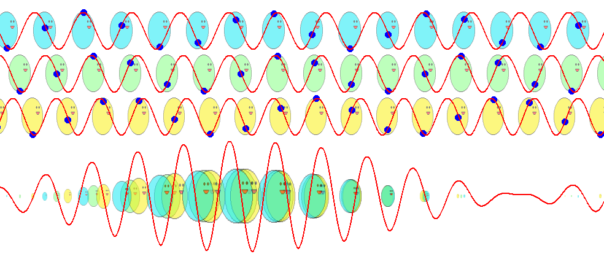
では、ド・ブロイが次に考えた位相波ならどうでしょうか? 位相波は粒子の周囲の空間に広がっており、位相速度\(V_\theta=c^2/v\)という光速を超えるスピードで進むと考えているのですから、半径\(r\)の軌道を一周する所要時間は、単純計算で
$$t=\frac{2\pi r}{V_\theta}=\frac{2\pi vr}{c^2}\tag{6.11}$$
となります。軌道を一周する間に進む位相は
$$2\pi \nu t=2\pi \frac{2\pi mvr}{h}\tag{6.12}$$
となり、これを\(2\pi\)の整数倍に限定すると
$$2\pi \frac{2\pi mvr}{h}=2\pi n\tag{6.14}$$
という量子条件が導かれます。両辺を\(h/(2\pi)\)倍すれば、
$$2\pi mvr=nh\;\;\;\;(今度は成功!)\tag{6.13}$$
ボーアの量子条件の式(\ref{bohr})と一致しました!
 式(\ref{balance})と式(\ref{bohr})から、軌道半径\(r\)とエネルギー\(E\)(運動エネルギーとクーロンポテンシャルの和)は、正の整数\(n\)をパラメータとして
式(\ref{balance})と式(\ref{bohr})から、軌道半径\(r\)とエネルギー\(E\)(運動エネルギーとクーロンポテンシャルの和)は、正の整数\(n\)をパラメータとして