完全拡散律速成長モデルでは、ドライ酸化にみられる初期異常の解釈がDeal-Groveモデルの場合と180度変わります。今回は、このことを詳しく見ていきましょう。
下図は、Deal-Groveモデルと完全拡散律速モデルを並べて比較したものです。微分方程式の概形は全く同じで、放物型定数\(B\)も同じ。違うのは定数\(A\)ですが、
$$\kappa \equiv \frac{D_0}{L\int_{x_0-L}^{x_0}\exp\left [\frac{\Delta E(x)}{k_BT}\right ]dx-L}\label{kappa}\tag{1}$$
とおけば、線形速度定数\(B/A\)の式もDeal-Grove方程式と見た目が一緒になります。「完全拡散律速モデルといっても単に界面反応速度定数\(k\)の解釈を変えただけで、何も新しくないじゃないか」と批判されてしまいそうですが・・・、果たしてそうでしょうか?
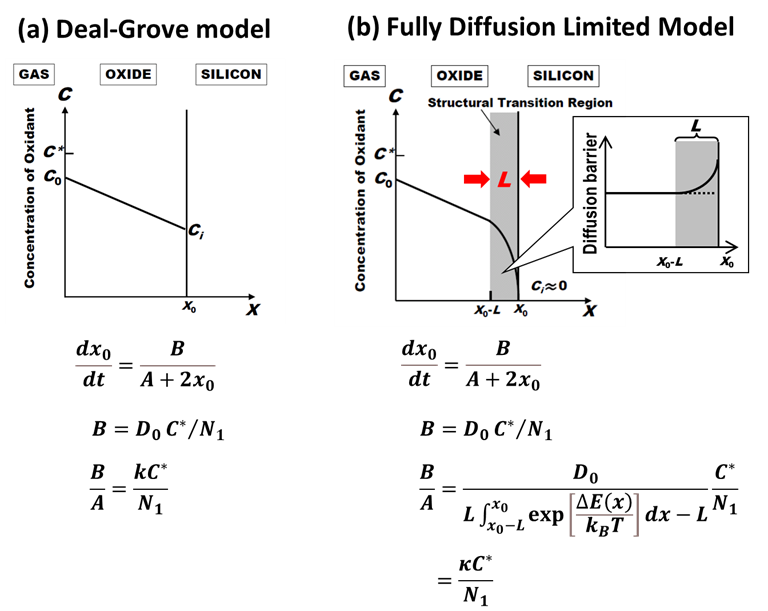
重要な変更点は、式\(\eqref{kappa}\)の速度定数\(\kappa\)が拡散係数\(D_0\)に比例するようになった点です。これにより、ドライ酸化にみられる初期異常の解釈がDeal-Groveモデルと変わってくるのです。
「Fargeixの解析」の回で、ドライ酸化の初期異常は、界面反応速度定数\(k\)が大きくなるか、あるいは拡散係数\(D_0\)が初期段階で低下していないと説明できない、という話をしました。DealとGroveは1965年の論文[1]で初期増速拡散説を唱えましたが、1983年のこのFargeixの解析[2]で否定されてしまったのです。
ところが、完全拡散律速モデルでは、この初期増速拡散説が復活します。Fargeixの解析にしたがって、酸化速度の逆数\(dt/dx_0\)の振る舞いを調べてみましょう。拡散係数\(D_0\)が酸化膜厚\(x_0\)に依存するとして、\(dt/dx_0\)を酸化膜厚\(x_0\)で微分すると
$$\begin{eqnarray}\frac{d}{dx_0}\left ( \frac{dt}{dx_0}\right ) &=&\frac{d}{dx_0}\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\\&=&\frac{d}{dx_0}\left ( \frac{A}{B}\right ) +\frac{d}{dx_0} \left (\frac{2}{B}\right )x_0+\frac{2}{B}\\&=&-\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\frac{1}{D_0} \frac{dD_0}{dx_0}+\frac{2}{B}\end{eqnarray}$$
となります。最後の式の第1項
$$-\left ( \frac{A}{B}+\frac{2}{B}x_0\right )\frac{1}{D_0} \frac{dD_0}{dx_0}$$
が初期異常による、線形-放物型曲線からのずれに相当します。Fargeixが示したように、酸化速度の逆数\(dt/dx_0\)の勾配は\(x_0\rightarrow 0\)で増大しますので、\(dD_0/dx_0 <0\)でないといけません。つまり、酸化膜厚が薄くなるほど\(D_0\)が増大しなければ初期異常を説明できなくなるのです。これはDeal-Grove方程式とは真逆の結論です。
[1] B. E. Deal, A. S. Grove, J. Appl. Phys. 36, 3770 (1965).
[2] A. Fargeix, G. Ghibaudo, G. Kamarinos, J. Appl. Phys. 54, 2878 (1983).