前回新たに導出した定式化した式をつかって、酸化速度の実験値を再現するような構造遷移領域の厚さ\(L\)を求めてみましょう。
新しい酸化速度方程式では、定数\(B\)はDeal-Grove方程式と一緒ですが、定数\(A\)は
$$A= 2\int_{x_0-L}^{x_0}\exp \left [ \frac{\Delta E(x)}{k_BT}\right ]dx-2L+2D_0/h\label{a}\tag{1}$$
のように、構造遷移領域の厚さ\(L\)と構造遷移領域内の拡散障壁の増分\(\Delta E(x)\)に依存します。様々な温度における\(A\)の実験値がDeal-Groveの論文[1]に載っていますから、\(\Delta E(x)\)を適当に仮定すれば、実験値から\(L\)を求めることができます。
式\(\eqref{a}\)の中で、\(2D_0/h\)は無視します。酸化膜中の酸化種の拡散係数\(D_0\)と比べて、気相物質輸送係数\(h\)の方が圧倒的に大きいからです。DealとGroveの論文[1]でもそう仮定して解析していますし、この仮定は全く問題ありません。
また、\(\Delta E(x)\)ですが、線形速度定数\(B/A\)の活性化障壁が2eVなので、SiO2/Si界面における拡散障壁が約2eVになっていると考えると、\(\Delta E(x_0)\)は活性化障壁2eVから、界面から十分離れた酸化膜中の拡散障壁1.24eVを引いた値となるので
$$\Delta E(x_0) = 2.0 – 1.24 = 0.76 ({\rm eV})$$
とおけます。
下の表に、\(\Delta E(x)\)の関数形をいくつか適当に仮定して計算した、定数\(A\)の実験値を再現する\(L\)の値を示します。温度によって変わりますが、概ね1nm弱になっていることがわかります。いろいろな実験で指摘されていた、SiO2/Si界面近傍の構造遷移領域の厚さと一致しているので、この完全拡散律速モデルの妥当性を裏付けていると言えるでしょう。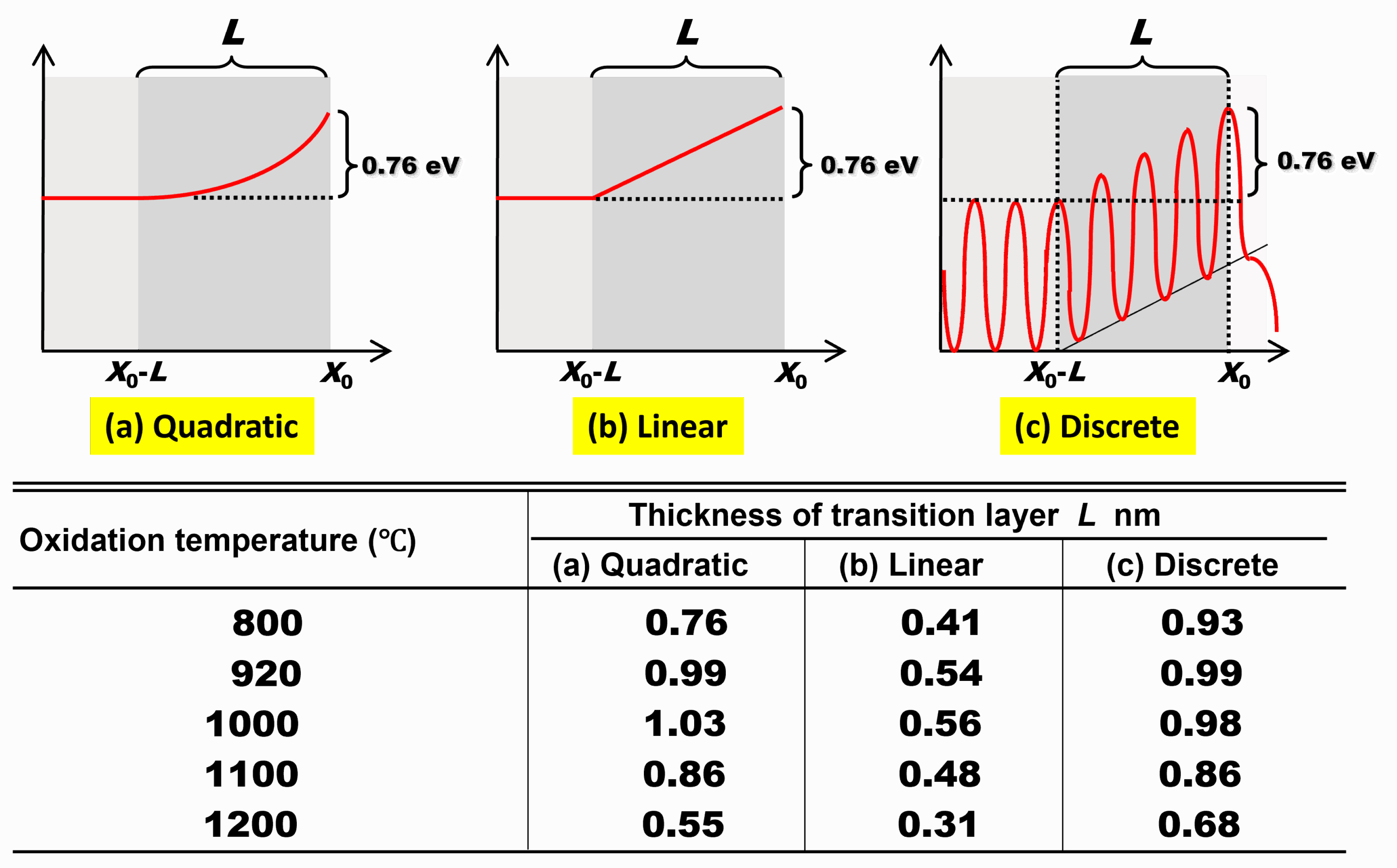
なお、(c)のDiscretizedモデルは、数原子層程度と非常に薄い構造遷移領域をよりリアルに表現するため、離散化した拡散モデルを用いた場合の結果です。導出は複雑になるのでここでは示していませんが、知りたい方は論文[2]をご覧ください。
[1] B. E. Deal, A. S. Grove, J. Appl. Phys. 36, 3770 (1965).
[2] T. Watanabe, K. Tatsumura, I. Ohdomari, Phys. Rev. Lett., 96, 196102 (2006).