渡邉孝信(早稲田大学・電子物理システム学科)
一般に、位相速度が異なる複数の波を重ねると、位相一致点で振幅が大きくなり、こぶ状の塊ができます。音波で言えば「うなり(beat)」という現象に相当します。周波数がわずかに異なる2つの音叉を鳴らしたとき、ウァン、ウァン、ウァンと、ゆっくり音の大きさが変わる現象が起きますが、あれがうなりです。うなりが生じているときの、波の振幅の膨らみのことを「波束(wave packet)」と呼びます。
波束の移動速度は、元の波の位相速度とはずいぶん異なります。
振動数\(\nu\)、波長\(\lambda\)をもつ単一の正弦波
$$\sin \left ( 2\pi \left (\nu t – \frac{x}{\lambda} \right ) \right )\tag{5.1}$$
の位相速度(phase velocity)\(V_\theta\)は
$$V_\theta = \lambda\nu\tag{5.2}$$
で与えられます。一方、波束の移動速度は「群速度(group velocity)」と呼び、
$$V_g = \frac{d\nu}{d(1/\lambda)}\label{vg}\tag{5.3}$$
で与えられます。式(\ref{vg})の導出は、次回以降の記事で示す予定です。今回のところは、式(\ref{vg})を天下り的に受け入れ、ド・ブロイの位相波がどんな群速度をもつか、調べてみましょう。
ド・ブロイの物質波理論では、質量\(m\)の粒子には\(\nu=mc^2/h\)という振動数が付随し、粒子と一緒に動く慣性系からみた位相波は
$$\sin(2\pi\nu t)=\sin\left ( 2\pi \frac{mc^2}{h}t\right )\tag{5.4}$$
とあらわされます。この粒子が速度\(v\)で移動すると、静止系から見たこの粒子の位相波は、ローレンツ変換を施すことで
$$\sin\left ( 2\pi \frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t -\frac{vx}{c^2}\right )\right )\tag{5.5}$$
に変わるのでした。よって静止系から見た位相波の振動数\(\nu\)と波長\(\lambda\)はそれぞれ、
$$\nu=\frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\tag{5.6}$$
$$\lambda=\sqrt{1-\frac{v^2}{c^2}}\frac{h}{mv}\tag{5.7}$$
で与えられます。位相波の位相速度は\(V_\theta=\lambda\nu=c^2/v\)ですから、異なる\(v\)の粒子に付随する位相波を重ねれば、波束を作ることができます。
振動数\(\nu\)と波長の逆数\(1/\lambda\)を\(v\)で微分すると、
$$\frac{d\nu}{dv}=\frac{mv}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}$$
$$\frac{d(1/\lambda)}{dv}=\frac{m}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}$$
となるので、群速度\(V_g\)は
$$V_g = \frac{d\nu}{d(1/\lambda)} = \frac{d\nu}{dv}\frac{dv}{d(1/\lambda)}=\frac{mv}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}\frac{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}{m}=v\tag{5.8}$$
となります。なんと、群速度は粒子の元の速度\(v\)になりました!
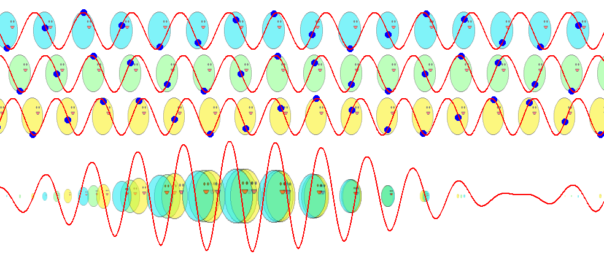
前回のアニメーションを改造して、波束の様子も描いてみました。上段の3つの波は、粒子の速度が上から順に\(v-\alpha\)、 \(v\) 、\(v+\alpha\) の場合の位相波です。これら3つの波の合成波を、最下段に示しています。
赤線の位相波はあきらかに粒子よりも速いスピードで前進していますが、3つの位相波を合成してできた波束のふくらみ(包絡線)に注目すると、そのピークは粒子の平均速度vと同じゆっくりとしたスピードで進んでいることがわかります。
このように、重ねる位相波の数をどんどん増やしていくと、波束は細くシャープになっていきます。無限個の位相波をうまく重ねた極限では、振幅の絶対値がデルタ関数のように空間の1点でピークを持つ波束に収縮すると考えられます。
この物質波のモデルに、量子力学の基本原理である「不確定性関係」がすでにあらわれていることは注目に値します。粒子の速度\(v\)をきっちり決めたいと思えば、波動の振動数はただ一つになって、空間に一様に広がる波になってしまいます。つまり、粒子が空間のどこに位置するか、決めることができなくなってしまいます。逆に、もし位置を限定したければ、様々な位相速度の波動を重ね合わせなければなりません。波束のピーク位置の移動速度は群速度なので確かに\(v\)となりますが、これはいわばたくさんの波群の統計平均的な速度\(\left < v \right >\)であって、位相速度と1対1対応する\(v\)は不確定になるのです。
※このページだけご覧になる方が誤解しないよう補足しますと、現在の標準的な物理学でド・ブロイの位相波は実在するものとは考えられておらず、ましてや粒子の正体が位相波の単純な合成だと考えられているわけでもありません。(分散のある波の)波束は時間とともに広がり散り散りになってしまうので、素朴に波が重ね合わさった状態と考えたのでは、常に粒子として1個、2個、・・・とカウントできる形で観測される事実を説明することは困難です。粒子の離散的な特徴を記述するには「場の量子論」が必要です。