渡邉孝信（早稲田大学・電子物理システム学科）

ドルーでも1/2倍していた！

係数に1/2倍の違いが生じる問題は、第２回で少し触れたように、ドリフト移動度\(\mu\)でも起こっていました。ドルーデが1900年に発表した古典的電気伝導理論の記念碑的論文で

$$\mu=\frac{q\overline{t}}{2m}　　（←間違い！）\label{half}\tag{5.1}$$

と定式化されていたのです（\(\overline{t}\)の定義の仕方によっては必ずしも間違いではないのですが、今となってはつけない方がよいでしょう）。この問題を掘り下げていくと、拡散係数の1/2倍の違いの原因も見えてきます。まず、ドリフト移動度についておさらいをしたのち、どうして移動度を式\(\eqref{half}\)で表したのか、式\(\eqref{half}\)がどうして誤りだという結論に至ったのか、見ていくことにしましょう。

 

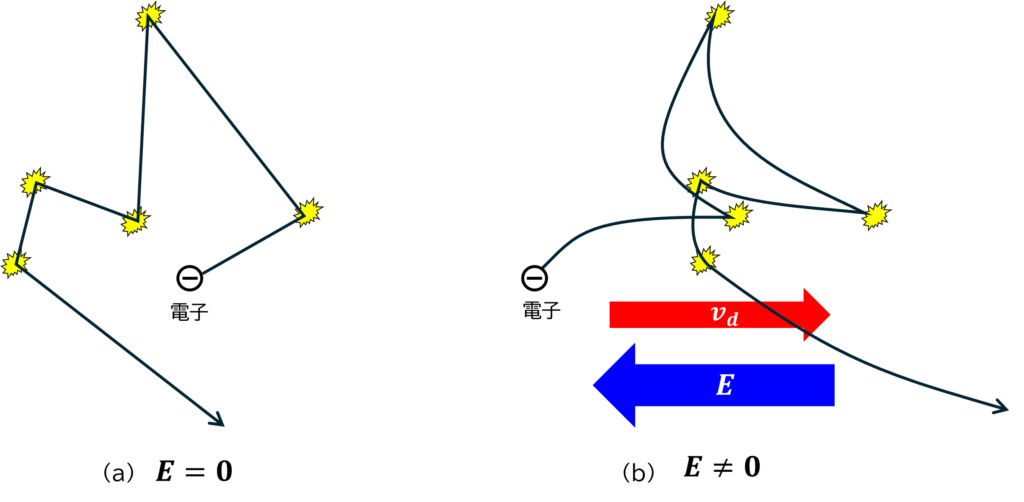
図5.1は、導体中の電子の運動の軌跡を模式的に示した図です。図5.1(a)は外から電界が印加されていない状態です。電子は熱エネルギーをもって絶えずブラウン運動していますが、不純物イオンやフォノンなどと衝突を起こす度に頻繁に移動方向を変え、移動方向は完全にランダムになります。時間平均を取ると特定の方向への移動はなくなり、正味の電流はゼロとなります。

図5.1(b)は、外部から電界を印加したときの様子です。この場合も電子はランダムな運動をしますが、衝突イベントと衝突イベントの間に電界によって加速されます。長時間平均を取ると、電子は定常的な速度\(\boldsymbol{v}_d\)で電界ベクトルの方向（と逆向き）に移動する傾向を示します。 \(\boldsymbol{v}_d\)がドリフト速度です。

電子のドリフト移動度\(\mu\) (cm\({}^2\)・V\({}^{-1}\)s\({}^{-1}\))は、次式で定義されます。

$$\mu\equiv -\frac{\boldsymbol{v}_d}{\boldsymbol{E}}\tag{5.2}$$

\(\boldsymbol{E}\)（V/cm）は外部から印加する電界です。この式、つまりドリフト速度を、平均自由時間\(\overline{t}\)を使った微視的な描像で定式化してみましょう。

今、外部電界\(E\)が\(x\)軸方向に一様に印加されているとし、個々の電子がニュートン方程式に従って運動するとみなすと、運動方程式の\(x\)成分は

$$m\frac{d v_x}{dt}=-qE\tag{5.3}$$

となります。時刻0における速度の\(x\)成分を\(v_x(0)\)とし、次の衝突が起こる前の時刻を\(t\)とすると、運動方程式の解は

$$m v_x(t)-mv_x(0)=-qEt\tag{5.4}$$

となります。これを多数の電子についてアンサンブル平均をとると、

$$m\left <v_x(t)-v_x(0)\right >=-qE\left<t\right>\tag{5.5}$$

となります。左辺の\(\left <v_x(t)-v_x(0)\right >\)は、衝突が起こらない間に獲得する速度の平均なので、これがドリフト速度 \(v_d\)とみなせます。右辺の\(\left < t\right >\)は、電界によって加速される時間のアンサンブル平均です。これを平均自由時間、すなわち\(\left<t\right>=\overline{t}\)とみなせば、

$$\mu=\frac{q\overline{t}}{m}　　（←正しい！）\tag{5.6}$$

となり、期待どおりのドリフト移動度の式が導かれます。

一方、最初に示した誤った式\(\eqref{half}\)では、 \(\left < t \right > =\overline{t}/2\)としていることになります。

どうして1/2倍したくなるのか？

ドルーデが\(\mu=q\overline{t}/2m\)を採用した最大の理由はおそらく、金属の電気伝導度と熱伝導度の比が温度に比例するというヴィーデマン・フランツ則が、\(\mu=q\overline{t}/2m\)とおくことで、当時の古典論の枠組みで定量的に説明できた（できてしまった）からだと想像されます。しかし、ドルーデほどの人が辻褄合わせをしたわけではないでしょうから、1/2倍した明確な根拠もあったはずです。

次のように考えれば1/2をつけたくなる気持ちが想像できます。

 

図5.2は、時間間隔\(\overline{t}\)で衝突する典型的な電子が、電界から獲得する速度と時間の関係を示したグラフです。前の衝突から次の衝突までの間、速度は時間に比例して増加します。衝突の度に速度はリセットされ、熱運動以外の速度成分はゼロとなります。すると、平均自由時間\(\overline{t}\)内に電界によって増える速度成分の時間平均は、最終的に獲得する速度\(qE\overline{t}/m\)の1/2となります。

至極まっとうな考え方に見えますが、一体この考え方のどこが良くないのでしょう？

図5.2のモデルの問題は、すべての電子が一定の時間間隔\(\overline{t}\)で衝突を起こす、という仮定にあります。

次の例を考えれば、1/2倍して平均値を得ることが一般性のない考え方とすぐにわかります。

 

図5.2は、衝突の時間間隔が\(t_1\)の場合と\(t_2\)の場合が同じ確率で起こる場合の例です。この時、獲得速度の平均は

$$\left <v_x(t)-v_x(0)\right >=-\frac{qE}{m}\frac{t_1^2+t_2^2}{2(t_1+t_2)}\tag{5.6}$$

となります。\(\overline{t}=(t_1+t_2)/2\)とおいても、式\(\eqref{half}\)にならないことは明らかでしょう。よって、すべての電子が一定の時間間隔\(\overline{t}\)で衝突を起こす、という不自然な仮定を設けるなら、1/2がつくのは正当化されますが、そうでなければ正当化されません。

これは言い換えれば、衝突イベントが起こるタイミングの確率分布に応じて、移動度の係数もいろいろ変化しうることを示唆しています。