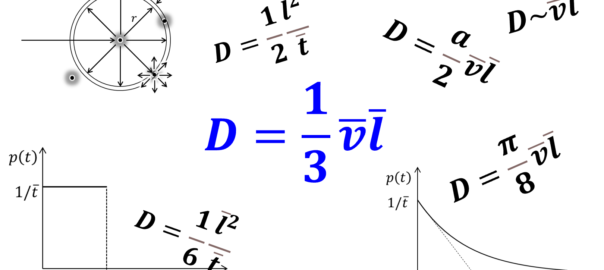渡邉孝信（早稲田大学・電子物理システム学科）

ドリフト移動度から拡散係数を決めてみる

ドリフト移動度\(\mu\)は、 \(q\)を素電荷、\(m\)を電子の質量（正確に言うと有効質量）、\(\overline{t}\)を平均自由時間として

$$\mu=\frac{q\overline{t}}{m} \tag{2.1}$$

と表されます。\(\mu=q\overline{t}/(2m)\)としていた本も以前にあったようですが、それは誤りだというのが現在の大方の見解です。

これはアシュクロフト-マーミン著「固体物理学の基礎」にも書かれている有名な話ですが、1900年に最初に電気伝導の古典的理論を発表したドルーデ自身、論文で\(\mu=q\overline{t}/(2m)\)と書いていました。その後、1905年に発表されたローレンツの論文で\(\mu=q\overline{t}/m\)に修正されたのです。

ドリフト移動度\(\mu\)に1/2をつけるか否かという問題はたいへん微妙で、アシュクロフト-マーミンの本でも第１章の最初の演習問題として取り上げて読者に熟考を促しています。実はこの問題が、ドリフト移動度だけでなく、拡散係数の式の違いにも関係してくる、というのがこのシリーズ記事を通して伝えたいことなのですが、この件については追々詳しく説明していきます。

　さて、ドリフト移動度\(\mu\)が決まっているなら、アインシュタインの関係式から

$$D=\frac{\mu}{q}k_BT=\frac{\overline{t}}{m}k_BT \tag{2.2}$$

と拡散係数\(D\)が一意に決まります。系が熱平衡状態に近く、エネルギーの等分配則

$$\frac{1}{2}m\overline{v^2}=\frac{3}{2}k_BT \label{equipartition}\tag{2.3}$$

が成り立つと考えてよければ、平均熱速度を根二乗平均速度として（\(\overline{v}=\sqrt{\overline{v^2}}\)）

$$D=\frac{1}{3}\overline{v^2}\overline{t}=\frac{1}{3}\overline{v}\overline{l}=\frac{\overline{l}^2}{3\overline{t}} \label{diffusivity}\tag{2.4}$$

となります。ここで\(\overline{l}=\overline{v}\overline{t}\)としました。

　ここで注意すべきことは、熱平衡状態で成り立つエネルギーの等分配則の式\(\eqref{equipartition}\)を仮定している点です。拡散電流が流れているときは熱平衡状態ではありませんから、マクスウェル・ボルツマン分布は歪んでいるはずで、等分配則も厳密には成り立ちません。式\(\eqref{diffusivity}\)はあくまで近似式に過ぎないことを忘れないようにしましょう。