渡邉孝信（早稲田大学・電子物理システム学科）

ここまでの話で、ド・ブロイの業績として有名な関係式

$$\lambda  = \frac{h}{p}\label{debroglie}\tag{7.1}$$

が、最初に紹介して以来、まだ一度も登場していません。実際、1924年に受理されたド・ブロイの博士論文でも、式(\ref{debroglie})について少ししか触れられていませんでした。

　ド・ブロイの関係式(\ref{debroglie})は、ド・ブロイが考えた位相波の位相速度

$$V_\theta = \frac{c^2}{v}\label{phasev}\tag{7.2}$$

から簡単に導くことができます。まず、波動現象で一般に成り立つ位相速度\(V_\theta\)の式

$$V_\theta=\lambda\nu\tag{7.3}$$

から出発します。\(\lambda\)は波長、\(\nu\)は振動数です。この式に、速度\(v\)で運動する粒子に付随する波動の振動数

$$\nu = \frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \tag{3.2 再掲}$$

と、ド・ブロイの位相波の位相速度の式(\ref{phasev})を代入すると、波長\(\lambda\)は

$$\lambda = \frac{h}{mv}\sqrt{1-\frac{v^2}{c^2}}\label{wavel}\tag{7.4}$$

となります。

　また、相対性理論によると、速度\(v\)で運動する質量\(m\)の物体の運動量は

$$p = \frac{mv}{\sqrt{1-\frac{v^2}{c^2}}}\label{momentum}\tag{7.5}$$

で与えられるので、式(\ref{wavel})と式(\ref{momentum})から、

$$\lambda  = \frac{h}{p}\label{debroglie2}\tag{7.6}$$

が導かれます。式(\ref{debroglie2})は、光速より速い位相速度\(V_\theta = {c^2}/{v}\)を包み隠してくれる、たいへん便利な式です。

　式(\ref{debroglie2})を出発点におけば、ボーアの量子条件も、半径\(r\)の円軌道が物質波の波長\(\lambda\)の整数倍でなければならないという条件

$$2\pi r=n\lambda\label{bohr}\tag{7.7}$$

から、簡単に導くことができます。実際、相対性理論のことは考えずに\(p=mv\)とおいて、式(\ref{debroglie2})を式(\ref{bohr})に代入すると、簡単にボーアの量子条件

$$2\pi mv r=nh\label{bohr2}\tag{7.8}$$

の式が導かれます。現在のほとんどの教科書で、この説明が用いられていると思います。

（次回につづく）

渡邉孝信（早稲田大学・電子物理システム学科）

　ド・ブロイが物質波理論を作り上げる過程で目標にしたのが、ボーアの水素原子模型で仮定された量子条件を、粒子に付随する振動の位相一致条件で説明することでした。

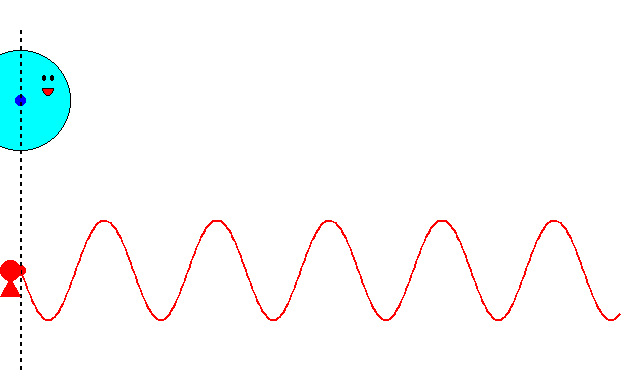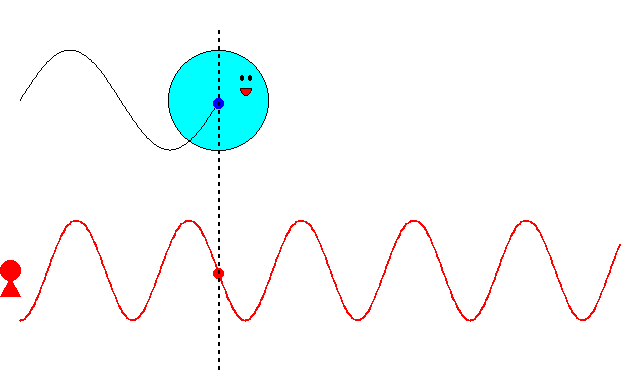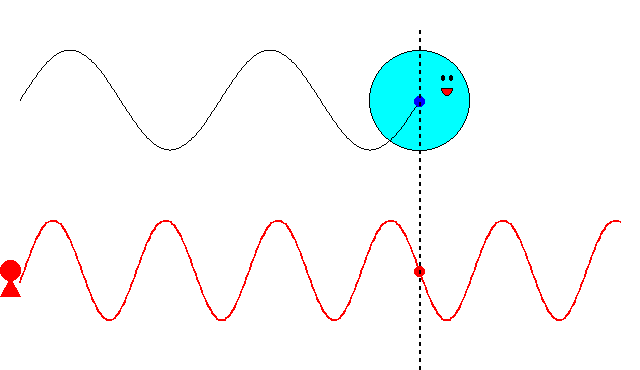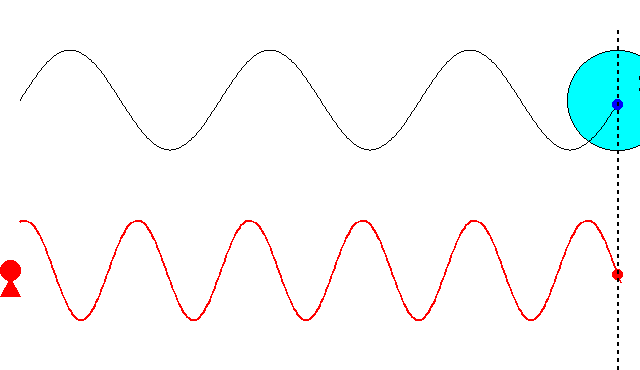
　これまでの記事で述べたように、最初ド・ブロイは、\(\nu=mc^2/h\)という振動数の振動現象が、「粒子の内部で」何らかの形で起こっていると考えていました。そして、この振動現象の位相が、原子核の周りを一周するごとに整数の周期分だけ変化すると想定しました。さもなければ、その軌道は不安定になるだろうと考えたからです。しかし、この考え方ではボーアの量子条件を導くことができませんでした。

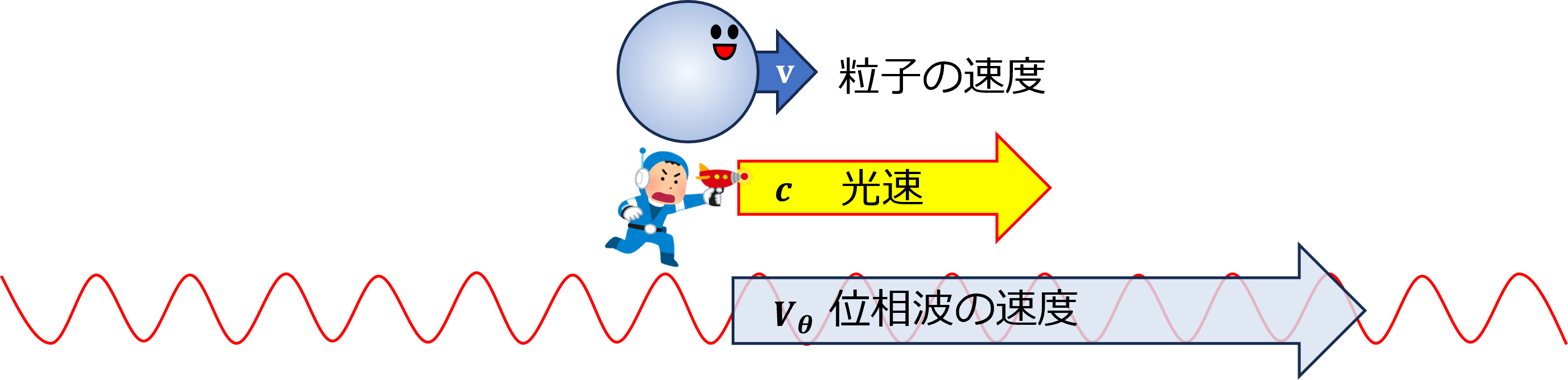
　その後、粒子の周囲の空間に広がる、光よりも速いスピードで粒子を先導する位相波という着想に至りました。この位相波が原子核の周りを一周するごとに整数の周期分だけ変化すると考えてみたところ、今度は見事、ボーアの量子条件を導くことに成功しました。これによりド・ブロイは、自身の物質波理論に確固たる自信をもったそうです。

　今回の記事では、ド・ブロイがボーアの量子条件を導けるようになるまでの経緯を追ってみたいと思います。

ボーアの水素原子モデル

　1913年に発表されたボーアの水素原子モデルでは、電子は原子核のまわりを円軌道に沿って周回すると考えます。電子の軌道が安定であるためには、電子が原子核から受けるクーロン力と、電子の周回運動による遠心力とが釣り合っていなければならないので

$$\frac{mv^2}{r}=\frac{q^2}{4\pi\varepsilon_0 r^2}\label{balance}\tag{6.1}$$

が成り立つ、とします。

　ボーアはさらに、「安定状態にある原子では、周回軌道に沿った電子の角運動量の積分がプランク定数\(h\)の整数倍になる」と仮定しました。すなわち

$$\oint P_\theta d\theta = \int_0^{2\pi}mvrd\theta = 2\pi mvr = nh\label{bohr}\tag{6.2}$$

と仮定したのです。右辺の\(n\)は正の整数です。この制約条件のおかげで、電子が取り得る軌道半径\(r\)とエネルギー\(E\)が、とびとびの離散的な値に限定されます。式(\ref{bohr})をボーアの量子条件と呼びます。

　式(\ref{balance})と式(\ref{bohr})から、軌道半径\(r\)とエネルギー\(E\)（運動エネルギーとクーロンポテンシャルの和）は、正の整数\(n\)をパラメータとして

$$r_n = \frac{\varepsilon_0 n^2 h^2}{\pi m q^2}\tag{6.3}$$

$$E_n = -\frac{mq^4}{8 \varepsilon_0^2 n^2 h^2}\label{Henergy}\tag{6.4}$$

と導かれます（クーロンポテンシャルは\(r\rightarrow\infty\)の極限でゼロとしています）。最も低い\(n=1\)の基底状態の半径は\(r_1=0.0529177\) nmで、ボーア半径と呼ばれます。基底エネルギーは\(E_1=-13.6057\) eVで、水素原子のイオン化エネルギーと一致します。

　高いエネルギー状態\(E_n\)から低い\(E_{n^\prime}\)に遷移する際（\(n>n^\prime\)）に光が放出されますが、この光の振動数\(\nu\)が、アインシュタインの光量子仮説\(E=h\nu\)より

$$E_n-E_{n^\prime}=h\nu \label{enen}\tag{6.5}$$

を満たす振動数に限定されるとすると、水素放電管で観察されるスペクトル線の波長を決める式「リュードベリの公式」を見事に説明できたのです。リュードベリの公式は

$$\frac{1}{\lambda}=R_{\infty}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)\;\;\;\;(n>n^\prime)\tag{6.6}$$

で与えられます。\(R_\infty\)はリュードベリ定数で、実験で\(1.0973\times10^7{\rm m}^{-1}\)と測定されていました。

　式(\ref{enen})にエネルギー準位の式(\ref{Henergy})を代入すると、

$$\begin{eqnarray}E_n-E_{n^\prime} &=& -\frac{mq^4}{8 \varepsilon_0^2 n^2 h^2}+\frac{mq^4}{8 \varepsilon_0^2 {n^\prime}^2 h^2}\\ &=&\frac{mq^4}{8\varepsilon_0 h^2}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)=h\nu\end{eqnarray}$$

となります。\(c=\lambda\nu\)より、

$$\frac{1}{\lambda}=\frac{\nu}{c}=\frac{mq^4}{8\varepsilon_0 h^3c}\left ( \frac{1}{{n^\prime}^2}-\frac{1}{{n}^2}\right)\;\;\;\;(n>n^\prime)\tag{6.7}$$

が得られます。\(\frac{mq^4}{8\varepsilon_0 h^3c}\)の数値は\(1.09737315\times10^7{\rm m}^{-1}\)となり、リュードベリ定数の実験値と一致します。

位相一致条件からボーアの量子条件を導く

　ボーアの水素原子モデルの成功のカギは、ボーアが仮定した量子条件の式(\ref{bohr})

$$ 2\pi mvr = nh\tag{6.2　再掲}$$

にあります。ド・ブロイは、粒子に付随する振動の位相が、原子核の周りを一周するごとに整数の周期分だけ変化するという条件で、式(\ref{bohr})を導こうとしたのです。

　ド・ブロイは当初、\(\nu=mc^2/h\)という振動数の振動現象が、電子の内部で起こっていると考えていました。電子の速度が\(v\)のとき、半径\(r\)の軌道を一周する所要時間は

$$t=\frac{2\pi r}{v}\tag{6.8}$$

ですから、軌道を一周する間に進む位相は

$$2\pi \nu t=2\pi \frac{2\pi mc^2}{vh}\tag{6.9}$$

となります。これが\(2\pi\)の整数倍に限定されるとすると

$$2\pi \frac{2\pi mc^2}{vh}=2\pi n\;\;\;\;（残念、失敗！）\tag{6.10}$$

という量子条件が導かれます。残念ながら、ボーアの量子条件の式(\ref{bohr})と一致しません。ここでは\(v\)は光速\(c\)より十分小さいとし、振動数にローレンツ因子はかけませんでしたが、たとえかけたとしてもボーアの量子条件にはなりません（円運動なのでそもそも特殊相対論の範疇を超えていますが）。

　では、ド・ブロイが次に考えた位相波ならどうでしょうか？　位相波は粒子の周囲の空間に広がっており、位相速度\(V_\theta=c^2/v\)という光速を超えるスピードで進むと考えているのですから、半径\(r\)の軌道を一周する所要時間は、単純計算で

$$t=\frac{2\pi r}{V_\theta}=\frac{2\pi vr}{c^2}\tag{6.11}$$

となります。軌道を一周する間に進む位相は

$$2\pi \nu t=2\pi \frac{2\pi mvr}{h}\tag{6.12}$$

となり、これを\(2\pi\)の整数倍に限定すると

$$2\pi \frac{2\pi mvr}{h}=2\pi n\tag{6.14}$$

という量子条件が導かれます。両辺を\(h/(2\pi)\)倍すれば、

$$2\pi mvr=nh\;\;\;\;（今度は成功！）\tag{6.13}$$

ボーアの量子条件の式(\ref{bohr})と一致しました！

　渡邉孝信（早稲田大学・電子物理システム学科）

　一般に、位相速度が異なる複数の波を重ねると、位相一致点で振幅が大きくなり、こぶ状の塊ができます。音波で言えば「うなり（beat）」という現象に相当します。周波数がわずかに異なる２つの音叉を鳴らしたとき、ウァン、ウァン、ウァンと、ゆっくり音の大きさが変わる現象が起きますが、あれがうなりです。うなりが生じているときの、波の振幅の膨らみのことを「波束（wave packet）」と呼びます。

　波束の移動速度は、元の波の位相速度とはずいぶん異なります。

　振動数\(\nu\)、波長\(\lambda\)をもつ単一の正弦波

$$\sin \left ( 2\pi \left (\nu t – \frac{x}{\lambda} \right ) \right )\tag{5.1}$$

の位相速度(phase velocity)\(V_\theta\)は

$$V_\theta = \lambda\nu\tag{5.2}$$

で与えられます。一方、波束の移動速度は「群速度（group velocity）」と呼び、

$$V_g = \frac{d\nu}{d(1/\lambda)}\label{vg}\tag{5.3}$$

で与えられます。式(\ref{vg})の導出は、次回以降の記事で示す予定です。今回のところは、式(\ref{vg})を天下り的に受け入れ、ド・ブロイの位相波がどんな群速度をもつか、調べてみましょう。

　ド・ブロイの物質波理論では、質量\(m\)の粒子には\(\nu=mc^2/h\)という振動数が付随し、粒子と一緒に動く慣性系からみた位相波は

$$\sin(2\pi\nu t)=\sin\left ( 2\pi \frac{mc^2}{h}t\right )\tag{5.4}$$

とあらわされます。この粒子が速度\(v\)で移動すると、静止系から見たこの粒子の位相波は、ローレンツ変換を施すことで

$$\sin\left ( 2\pi \frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t -\frac{vx}{c^2}\right )\right )\tag{5.5}$$

に変わるのでした。よって静止系から見た位相波の振動数\(\nu\)と波長\(\lambda\)はそれぞれ、

$$\nu=\frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\tag{5.6}$$

$$\lambda=\sqrt{1-\frac{v^2}{c^2}}\frac{h}{mv}\tag{5.7}$$

で与えられます。位相波の位相速度は\(V_\theta=\lambda\nu=c^2/v\)ですから、異なる\(v\)の粒子に付随する位相波を重ねれば、波束を作ることができます。

　振動数\(\nu\)と波長の逆数\(1/\lambda\)を\(v\)で微分すると、

$$\frac{d\nu}{dv}=\frac{mv}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}$$

$$\frac{d(1/\lambda)}{dv}=\frac{m}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}$$

となるので、群速度\(V_g\)は

$$V_g = \frac{d\nu}{d(1/\lambda)} = \frac{d\nu}{dv}\frac{dv}{d(1/\lambda)}=\frac{mv}{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}\frac{h{\left ( 1-\frac{v^2}{c^2}\right )}^{3/2}}{m}=v\tag{5.8}$$

となります。なんと、群速度は粒子の元の速度\(v\)になりました！

　前回のアニメーションを改造して、波束の様子も描いてみました。上段の３つの波は、粒子の速度が上から順に\(v-\alpha\)、 \(v\) 、\(v+\alpha\) の場合の位相波です。これら３つの波の合成波を、最下段に示しています。

赤線の位相波はあきらかに粒子よりも速いスピードで前進していますが、３つの位相波を合成してできた波束のふくらみ（包絡線）に注目すると、そのピークは粒子の平均速度vと同じゆっくりとしたスピードで進んでいることがわかります。

位相波の数を５つに増やすと、、、

　さらに増やすと、、、

このように、重ねる位相波の数をどんどん増やしていくと、波束は細くシャープになっていきます。無限個の位相波をうまく重ねた極限では、振幅の絶対値がデルタ関数のように空間の１点でピークを持つ波束に収縮すると考えられます。

　この物質波のモデルに、量子力学の基本原理である「不確定性関係」がすでにあらわれていることは注目に値します。粒子の速度\(v\)をきっちり決めたいと思えば、波動の振動数はただ一つになって、空間に一様に広がる波になってしまいます。つまり、粒子が空間のどこに位置するか、決めることができなくなってしまいます。逆に、もし位置を限定したければ、様々な位相速度の波動を重ね合わせなければなりません。波束のピーク位置の移動速度は群速度なので確かに\(v\)となりますが、これはいわばたくさんの波群の統計平均的な速度\(\left < v \right >\)であって、位相速度と１対１対応する\(v\)は不確定になるのです。

※このページだけご覧になる方が誤解しないよう補足しますと、現在の標準的な物理学でド・ブロイの位相波は実在するものとは考えられておらず、ましてや粒子の正体が位相波の単純な合成だと考えられているわけでもありません。（分散のある波の）波束は時間とともに広がり散り散りになってしまうので、素朴に波が重ね合わさった状態と考えたのでは、常に粒子として１個、２個、・・・とカウントできる形で観測される事実を説明することは困難です。粒子の離散的な特徴を記述するには「場の量子論」が必要です。

渡邉孝信（早稲田大学・電子物理システム学科）

位相一致の法則の式

$$2\pi\nu_1 t = 2 \pi \nu_2\left ( t-\frac{x}{V_\theta}\right )\tag{3.3 再掲} $$

を、ローレンツ変換を念頭において再検討してみましょう。

　ある慣性系\(S\)の時空座標を\((t,x,y,z)\)、\(S\)に対して相対速度\(v\)で\(x\)軸方向に移動する別の慣性系\(S^\prime\)の時空座標を\((t^\prime, x^\prime,y^\prime,z^\prime)\)とすると、両座標系は次のローレンツ変換で関連づけられます：

$$\begin{eqnarray}t^\prime &= & \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left (t-\frac{vx}{c^2} \right )\label{lorentz}\tag{4.1}\\x^\prime &= & \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( x-vt\right )\tag{4.2}\\y^\prime&=&y\tag{4.3}\\z^\prime&=&z\tag{4.4}\end{eqnarray}$$

　ここで、慣性系\(S^\prime\)において

$$\sin (2\pi\nu^\prime t^\prime)\label{sinewave}\tag{4.5}$$

という振動現象が起こっているとしましょう。式(\ref{sinewave})の正弦波は\(x^\prime\)を含んでいませんが、あえて

$$\sin \left (2\pi\nu^\prime t^\prime-2\pi\frac{x^\prime}{\infty}\right )\tag{4.6}$$

と書けば、これは波長無限大の波、つまり\(x^\prime\)軸上で一様な振動現象を表していることになります。

　この正弦波にローレンツ変換の式(\ref{lorentz})を適用すると、

$$\sin (2\pi\nu^\prime t^\prime)=\sin \left ( 2\pi \nu^\prime \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t-\frac{vx}{c^2}\right )  \right)\label{sinewave2}\tag{4.7}$$

となります。\( \nu=\nu^\prime\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)、\( V_\theta=\frac{c^2}{v} \)とおくと、式(\ref{sinewave2})の位相部分は

$$2\pi\nu^\prime t^\prime = 2\pi\nu\left ( t-\frac{x}{V_\theta}\right )\label{phasematching2}\tag{4.8}$$

と書けます。前回示した位相一致の法則の式

$$2\pi\nu_1 t = 2 \pi \nu_2\left ( t-\frac{x}{V_\theta}\right )\label{phasematching}\tag{3.3} $$

とよく似てきました。

　前回の議論では

$$\nu_1=\frac{mc^2}{h}\sqrt{1-\frac{v^2}{c^2}},\;\;\; \nu_2=\frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$

としていたので、これを式(\ref{phasematching})に代入してみます。

$$2\pi\frac{mc^2}{h}\sqrt{1-\frac{v^2}{c^2}} t = 2 \pi \frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t-\frac{x}{V_\theta}\right )\tag{4.9}$$

ここで、粒子と一緒に動く慣性系\(S^\prime\)から見た、粒子に付随する振動数を\(\nu^\prime=\frac{mc^2}{h}\)とおくと、さきほど定義した\( \nu=\nu^\prime\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)も使って、

$$2\pi\nu^\prime t \sqrt{1-\frac{v^2}{c^2}} = 2 \pi \nu\left ( t-\frac{x}{V_\theta}\right )\tag{4.10}$$

が得られます。\( t\sqrt{1-\frac{v^2}{c^2}}\)は\(S^\prime\)系の固有時間なので、\(t^\prime = t\sqrt{1-\frac{v^2}{c^2}}\)とおけます。これで

$$2\pi\nu^\prime t ^\prime = 2 \pi \nu\left ( t-\frac{x}{V_\theta}\right )\tag{4.11}$$

となり、式(\ref{phasematching2})と一致しました。

　このように「位相一致の法則」は、波の位相がローレンツ変換で変わらないという、当然の要請のことを言っているに過ぎないことがわかります。空間に広がって伝搬する波動のローレンツ変換ですから、位相一致は空間のあらゆる地点で起こっていることになります。

　以上の議論を踏まえて、位相一致の法則のアニメーションをブラッシュアップしてみました。今度は粒子内部の振動と位相波を重ねて示し、位相一致の法則が空間のいたるところで成立することがわかるよう、横にたくさん粒子を並べています。

　縦に複数の波を並べたのは、速度\(v\)との関係を示すためです。最上段は\(v=0\)、すなわち、\(S^\prime=S\)の特殊ケースです。下段に行くほど、粒子の速度\(v\)が光の速度に近づきます。ローレンツ収縮を意識して、粒子の幅も進行方向に縮めて示しています。粒子の速度\(v\)が大きくなると、赤線で示した位相波の振動数は増えていきますが、位相一致点の青玉の振動は、時間の遅れを反映した、ゆっくりした動きになっていきます。

　以上のように、粒子に\(h\nu=mc^2\)で振動数を結び付け、なおかつ、この粒子が速度\(v\)で運動した際のローレンツ変換とも整合する振動現象の描像を得ることができました。

　速度\(v\)で運動する粒子との位相一致点は、上のアニメーションで示したとおり、空間上のあらゆる点にとることができます。もし、先に波動が与えられたとして、空間の特定の位置を占めつつ運動する粒子の描像を得るにはどうしたらよいのでしょうか？

　ヒントはすでに、このページの一番上の、アイキャッチ画像に示してあります。次回、いよいよ波束（ウェーブパケット）の群速度と粒子の描像の関係について説明します。

渡邉孝信（早稲田大学・電子物理システム学科）

熟考の末、ド・ブロイは矛盾を解決するアイデアを思いつきました。それが、今回紹介する「位相一致の法則」です。

位相一致の法則

速度\(v\)で移動する粒子の内部で振動現象が起こっており、その振動数は静止系からみて

$$\nu_1 = \frac{m_0c^2}{h}\sqrt{1-\frac{v^2}{c^2}}\tag{3.1}$$

とする。この振動の位相は、位相速度\(V_\theta=c^2/v\)で前進する

$$\nu_2 = \frac{m_0c^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\tag{3.2}$$

という振動数をもつ波の位相と、粒子が存在するその１点において常に一致する。すなわち、

$$2\pi \nu_1t = 2\pi \nu_2\left ( t-\frac{x(t)}{V_\theta}\right )\tag{3.3}$$

ここで\(x(t)\)は、静止系の時間\(t\)の間に粒子が進む距離。

この位相一致の法則のイメージをアニメーションで示すと、こんな感じです。

上段が速度\(v\)で移動する粒子。その粒子の中で上下運動している青玉は、振動数

$$\nu_1 = \frac{m_0c^2}{h}\sqrt{1-\frac{v^2}{c^2}}$$

で振動しています。

　一方、下段の赤い波が、位相速度\(V_\theta=c^2/v\)で前進する

$$\nu_2 = \frac{m_0c^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$

という振動数の波です。

　上段の青玉と下段の赤線で示した進行波は、全く異なる振動数で振動しているのですが、速度\(v\)で前進する粒子の位置、その１点に注目してみると、位相が完全に一致していて、同期していることがわかります。

　位相一致の法則の証明はむずかしくありません。

位相一致の法則の証明

時間\(t\)の間に粒子が進む距離\(x\)は\(x=vt\)だから、\(t=x/v\)。よって振動数\(\nu_1\)で振動する波の位相は、時間\(t\)の間に

$$2\pi\nu_1t=2\pi\frac{m_0c^2}{h}\sqrt{1-\frac{v^2}{c^2}}\frac{x}{v}\tag{3.4}$$

だけ進む。一方、

$$\nu_2\left ( t-\frac{x}{V_\theta} \right ) = \frac{m_0c^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( \frac{x}{v}-\frac{vx}{c^2}\right )=\frac{m_0c^2}{h}\sqrt{1-\frac{v^2}{c^2}}\frac{x}{v}\tag{3.5}$$

であるから、

$$2\pi  \nu_1t =2\pi \nu_2\left ( t-\frac{x(t)}{V_\theta}\right )\tag{3.6}$$

が成り立つ。Q.E.D.

　以上から、ド・ブロイが\(h\nu=mc^2\)で結び付けたかった振動現象は、上のアニメーションで赤線で示した、粒子の周辺の空間に広がる波であればよさそうなことがわかってきました。この波は、位相速度\(V_\theta=c^2/v\) で粒子と同じ方向に、粒子を先導するかのように進みます。粒子の速度\(v\)と関係しているのです。この位相速度\(V_\theta=c^2/v\) の波を、ド・ブロイは「位相波」と名付けました。粒子の速度は観測者によって変わりますから、位相波が進む速度も観測者によって異なることになります。

　注意していただきたいのは、この位相波の速度\(V_\theta=c^2/v\) は光よりも速いことです。相対性理論によると、物体が光の速度を超えることは許されないので、ド・ブロイは、この位相波はエネルギーや情報を運ぶことは決してないだろうといっています。

　位相波の速度\(V_\theta=c^2/v\) は、\(v\)が大きくなるほど減少し、\(v=c\)の極限で\(V_\theta=c\)となります。粒子の速度と位相波の速度が一致するのです。ド・ブロイは光学と力学の統一を目指していたので、光子にもこの関係が適用できると考えていました。現在の物理学では、光子の質量はゼロというのが標準的な考え方ですが、ド・ブロイは、光子にもごくわずかなから質量があると考えていたようで、光子の速度\(v\)はいわゆる光速度\(c\)より若干遅く（おかしな言い方ですが）、光子の位相波は、光子よりほんの少しだけ速く進むと考えていました^[1]。

※このページだけご覧になる方が誤解しないよう補足しますと、ド・ブロイが考えたこの位相波は実在するものとは考えられておらず、現在の標準的な物理学で正しい理論と考えられているわけでもありません。ですが近年、幾何学的位相という概念を用いて説明される物質相が認識されているように、位相に注目するド・ブロイの着想を振り返ることには意義があるんじゃないかなと、筆者は思っています。

[1] ジョルジュ・ロシャク著，宇田川博訳「ルイ・ド・ブロイ　二十世紀物理学の貴公子」国文社（1995）

渡邉孝信（早稲田大学・電子物理システム学科）

　ド・ブロイがなぜ、電子も波動性を有するという、とてつもない着想に至ったかというと、光学と力学の理論の類似点に注目し、これらはいつか統合されなければならないという、壮大な構想を抱いていたからでした。

　光線がたどる経路を扱う理論を「幾何光学」と呼びます。幾何光学では、光は通過時間が極小値を通るような最短経路をたどると説明されます。フェルマーの原理と呼ばれます。

　一方、ニュートン力学では、その後に発展した解析力学によって、質点の運動は「作用量が極小値を取る」という意味で最短経路をたどっていると説明できることが明らかにされました。

　ド・ブロイは、これら最短経路の原理を基に、光学と力学とを一つに統合できるはずだと考えていたのです。もっとも、光学と力学のアナロジーを指摘していた人はド・ブロイ以前にもいましたが、実際に統合する手段が、昔はなかったのです。その手段というのが、後から振り返ると、アインシュタインの「光量子仮説」と「相対性理論」だった、ということになります。

　ド・ブロイは、アインシュタインの光量子仮説の式、

$$E=h\nu$$

すなわち振動数\(\nu\)の波のエネルギーの最小単位は\(h\nu\)だという式と、相対性理論の有名な式、

$$E=mc^2$$

をイコールとおいて、質量\(m\)を有するあらゆる物質粒子には、\(mc^2/h\)という振動数の振動現象が付随している、という前提から議論を始めました。

「粒子に振動現象が付随する」といわれても、なかなかピンとこないでしょう。ド・ブロイが実際にどのようなイメージを持っていたのか、詳細な描像は筆者にはわかりませんが、たぶん、最初はこんなイメージを持っていたのではないかと、勝手な想像を加えながら話を進めます。

図2.2に示すように、一定の振動数\(\nu_0\)で振動する何らかの機構、例えばメトロノームみたいなものが、静止質量\(m_0\)の粒子に内在していると考えてみましょう。前回紹介した、ニュートンの光の粒子の描像（光の粒子が透過状態と反射状態を繰り返しているという、アレです）を彷彿とさせるかもしれませんね。

　ド・ブロイは、この粒子が速度\(v\)で運動しているとして、内部の振動現象がどのように見えるだろうか、ということを、相対性理論に基づいて考察しました。

　相対性理論によると、静止系の時間を\(t_0\)とおいたとき、速度\(v\)で動いている物体の時間は

$$t_0\sqrt{1-\frac{v^2}{c^2}}$$

となります。\(c\)は光の速度です。\(v\)は光速を超えることはなく、平方根は1より小さな実数値になります。

　すなわち、静止している観測者から見て、動いている物体の時間はゆっくり進むことになります。時間がゆっくり進むなら、動いている粒子の内部の振動数も低下するはずです。

さて、今度は物体の質量に注目してみましょう。相対性理論によると、静止質量\(m_0\)の物体が速度\(v\)で動くと、その質量は

$$m_0\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$

となります。速度が増すほど質量は増えるのです。

　そうなると、ここで矛盾が生じます。質量\(m\)に付随する振動数が

$$\frac{mc^2}{h}$$

だとすると、質量が増えるにつれて振動数も増えなければなりません。時間の遅れに注目すると、粒子に付随する振動数は減るはずなのですが、質量の増大に注目すると、逆にこの振動数は増えてくれないと困ることになります。

　筆者ならここで、「ダメだ。\(E=hν\)と\(E=mc^2\)をイコールで結ぶなんて、やっぱりナンセンスだったんだ」とあきらめてしまうところです。しかし、ド・ブロイはあきらめませんでした。

「そのとき、大いなる光が頭のなかで　突然に輝きわたった」^[1]

と、後の回想録でド・ブロイが語っているように、この矛盾を見事に解消する、画期的な描像をド・ブロイは思いついたのでした。

[1] ジョルジュ・ロシャク著，宇田川博訳「ルイ・ド・ブロイ　二十世紀物理学の貴公子」国文社（1995）

渡邉孝信（早稲田大学・電子物理システム学科）

　半導体中の電気の流れを説明するとき、電子を粒子と見立てて説明されることが多いのですが、時として波動とみなした説明もされることがあります。電子をはじめ、光も、原子核も、この世のありとあらゆるものが、波動性と粒子性を兼ね備えているという話は、量子力学を学んでいなくても一度は聞いたことがあるでしょう。

　電子は19世紀末、真空放電で陰極から放射される放射線「陰極線」の実験で発見されました。1897年、陰極線の正体がとても小さな荷電粒子らしいことをＪＪトムソンが突き止めたので、この年が電子の発見年とされています。

　一方、光は波だと当時考えられていました。1864年にマクスウェルが確立した電磁気学によって、光が電磁波の一種であることが明らかになっていたからです。

　もっと時代をさかのぼると、ニュートンは光を粒子だと考えていました。波の干渉模様として知られるニュートン環を研究した当の本人が、光を粒子と想定していたとは、意外に思われるかも知れません。ニュートンは、レンズ間の薄い空気層に侵入した光線が、何らかの原因によって、反射される状態と透過する状態に繰り返し変化していると仮定し、ニュートン環の現象を説明したのです。

　ニュートン以後、ヤングの干渉縞の実験、マクスウェルの電磁気学によって、光は波だということが決定的になっていったのですが、1900年のプランクの量子仮説、1905年のアインシュタインの光量子仮説あたりから、光の素性について議論が再燃しました。

　そんな中で現れたのが、ド・ブロイの物質波理論です。ド・ブロイは1923年、光どころか、これまで粒子と考えられてきた電子も波の性質を持っている、と言い出しました。そして、アインシュタインが1917年に光量子に対して導いた運動量と波長の関係式

$$\lambda = \frac{h}{p} \tag{1.1}$$

が、電子のような物質粒子にも一般に成り立つ、と主張したのです。これを物質波理論と言います。この物質波理論がきっかけの一つとなって、シュレディンガーの波動方程式が誕生し、今の量子力学の基礎が固まりました（なお、シュレディンガー方程式が発表された1926年の前年、ハイゼンベルクが行列力学を発見した1925年が、量子力学の誕生の年とされています）。

　ド・ブロイの物質波理論では、アインシュタインの光量子仮説の式

$$E = h\nu \tag{1.2}$$

と、相対性理論の有名な式、

$$E=mc^2 \tag{1.3}$$

を等しいとおき、

質量\(m\)の粒子には、振動数\(\nu=mc^2/h\)の振動現象が付随しているのではないか

という着想から出発して理論が構築されました^[2]。

　「粒子に付随する振動現象」とは、いったい、どんなイメージを抱けばよいのでしょうか？

　筆者がこのシリーズ記事を書いている2024年は、ド・ブロイが物質波の理論をまとめた博士論文[3]が受理された年からちょうど100年の節目にあたります。それが動機、というわけでもないのですが、たまたま振り返る機会がありましたので、ド・ブロイの発見の道筋を、一部想像も交えながら再現してみようと思った次第です。

参考文献
[1] ニュートン著, 島尾永康訳,「光学」岩波書店 (1983).
[2] ジョルジュ・ロシャク著，宇田川博訳「ルイ・ド・ブロイ　二十世紀物理学の貴公子」国文社（1995）
[3] Louis-Victor de Broglie , “On the Theory of Quanta” ド・ブロイの博士学位論文(1924)の英訳