渡邉孝信(早稲田大学・電子物理システム学科)
位相一致の法則の式
$$2\pi\nu_1 t = 2 \pi \nu_2\left ( t-\frac{x}{V_\theta}\right )\tag{3.3 再掲} $$
を、ローレンツ変換を念頭において再検討してみましょう。
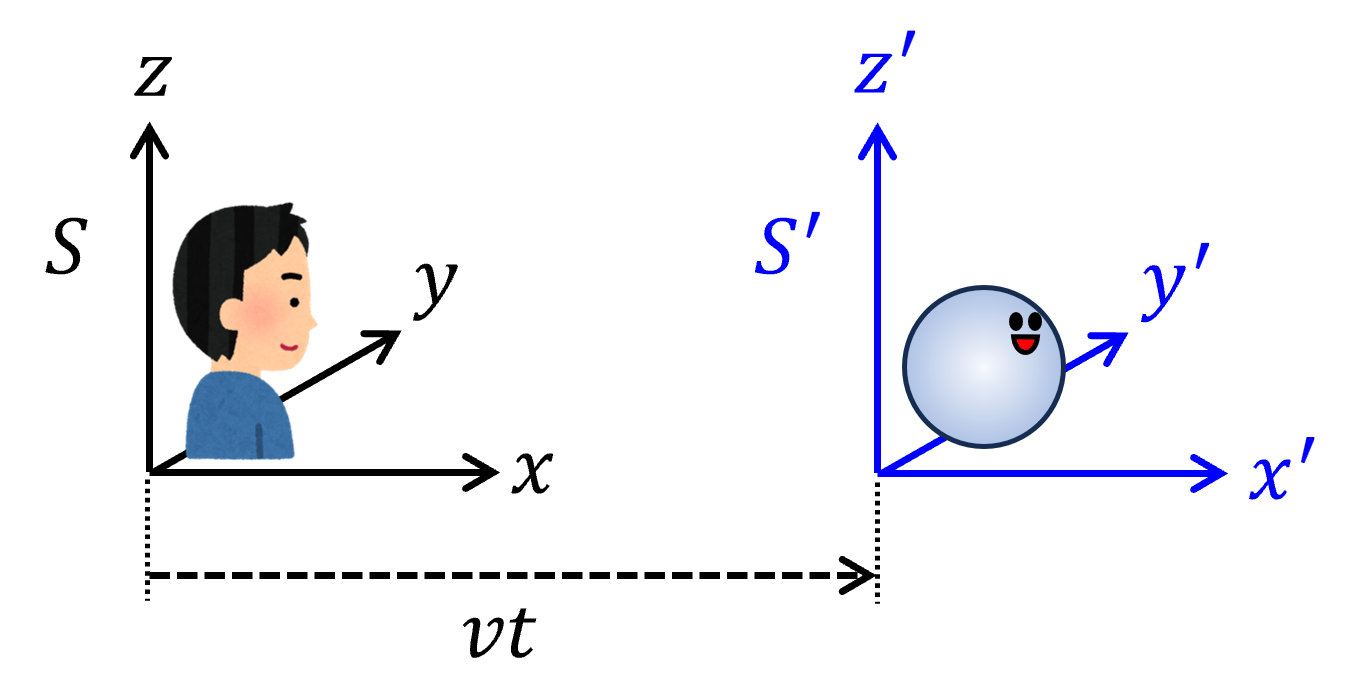
ある慣性系\(S\)の時空座標を\((t,x,y,z)\)、\(S\)に対して相対速度\(v\)で\(x\)軸方向に移動する別の慣性系\(S^\prime\)の時空座標を\((t^\prime, x^\prime,y^\prime,z^\prime)\)とすると、両座標系は次のローレンツ変換で関連づけられます:
$$\begin{eqnarray}t^\prime &= & \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left (t-\frac{vx}{c^2} \right )\label{lorentz}\tag{4.1}\\x^\prime &= & \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( x-vt\right )\tag{4.2}\\y^\prime&=&y\tag{4.3}\\z^\prime&=&z\tag{4.4}\end{eqnarray}$$
ここで、慣性系\(S^\prime\)において
$$\sin (2\pi\nu^\prime t^\prime)\label{sinewave}\tag{4.5}$$
という振動現象が起こっているとしましょう。式(\ref{sinewave})の正弦波は\(x^\prime\)を含んでいませんが、あえて
$$\sin \left (2\pi\nu^\prime t^\prime-2\pi\frac{x^\prime}{\infty}\right )\tag{4.6}$$
と書けば、これは波長無限大の波、つまり\(x^\prime\)軸上で一様な振動現象を表していることになります。
この正弦波にローレンツ変換の式(\ref{lorentz})を適用すると、
$$\sin (2\pi\nu^\prime t^\prime)=\sin \left ( 2\pi \nu^\prime \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t-\frac{vx}{c^2}\right ) \right)\label{sinewave2}\tag{4.7}$$
となります。\( \nu=\nu^\prime\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)、\( V_\theta=\frac{c^2}{v} \)とおくと、式(\ref{sinewave2})の位相部分は
$$2\pi\nu^\prime t^\prime = 2\pi\nu\left ( t-\frac{x}{V_\theta}\right )\label{phasematching2}\tag{4.8}$$
と書けます。前回示した位相一致の法則の式
$$2\pi\nu_1 t = 2 \pi \nu_2\left ( t-\frac{x}{V_\theta}\right )\label{phasematching}\tag{3.3} $$
とよく似てきました。
前回の議論では
$$\nu_1=\frac{mc^2}{h}\sqrt{1-\frac{v^2}{c^2}},\;\;\; \nu_2=\frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
としていたので、これを式(\ref{phasematching})に代入してみます。
$$2\pi\frac{mc^2}{h}\sqrt{1-\frac{v^2}{c^2}} t = 2 \pi \frac{mc^2}{h}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\left ( t-\frac{x}{V_\theta}\right )\tag{4.9}$$
ここで、粒子と一緒に動く慣性系\(S^\prime\)から見た、粒子に付随する振動数を\(\nu^\prime=\frac{mc^2}{h}\)とおくと、さきほど定義した\( \nu=\nu^\prime\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\)も使って、
$$2\pi\nu^\prime t \sqrt{1-\frac{v^2}{c^2}} = 2 \pi \nu\left ( t-\frac{x}{V_\theta}\right )\tag{4.10}$$
が得られます。\( t\sqrt{1-\frac{v^2}{c^2}}\)は\(S^\prime\)系の固有時間なので、\(t^\prime = t\sqrt{1-\frac{v^2}{c^2}}\)とおけます。これで
$$2\pi\nu^\prime t ^\prime = 2 \pi \nu\left ( t-\frac{x}{V_\theta}\right )\tag{4.11}$$
となり、式(\ref{phasematching2})と一致しました。
このように「位相一致の法則」は、波の位相がローレンツ変換で変わらないという、当然の要請のことを言っているに過ぎないことがわかります。空間に広がって伝搬する波動のローレンツ変換ですから、位相一致は空間のあらゆる地点で起こっていることになります。
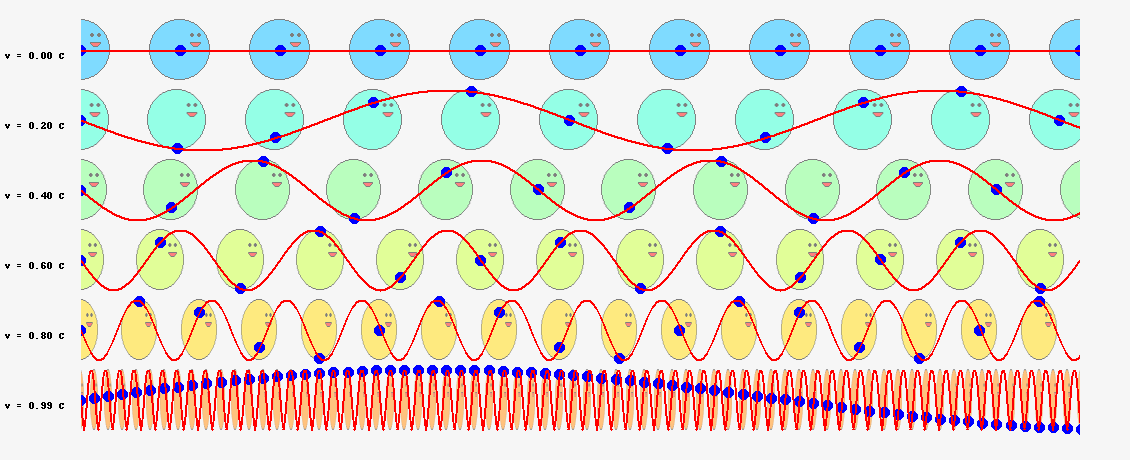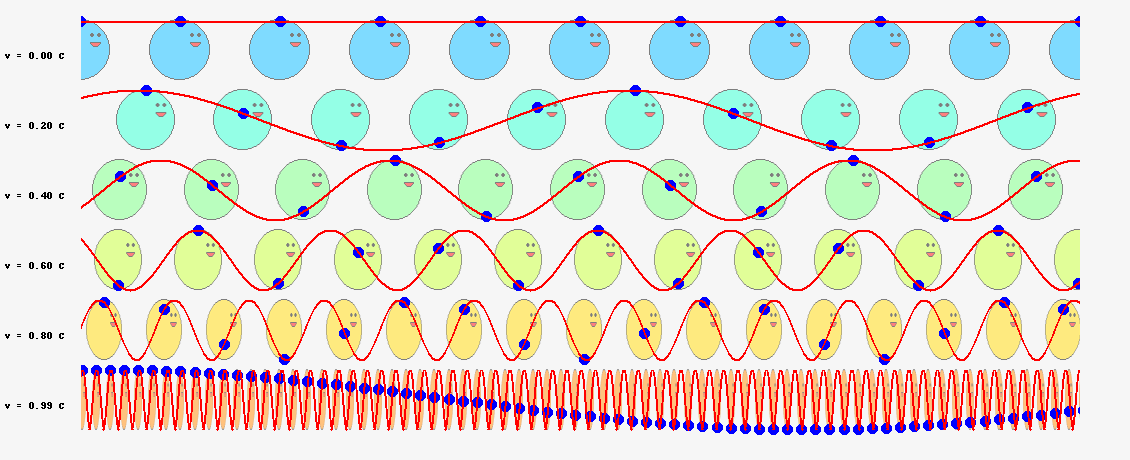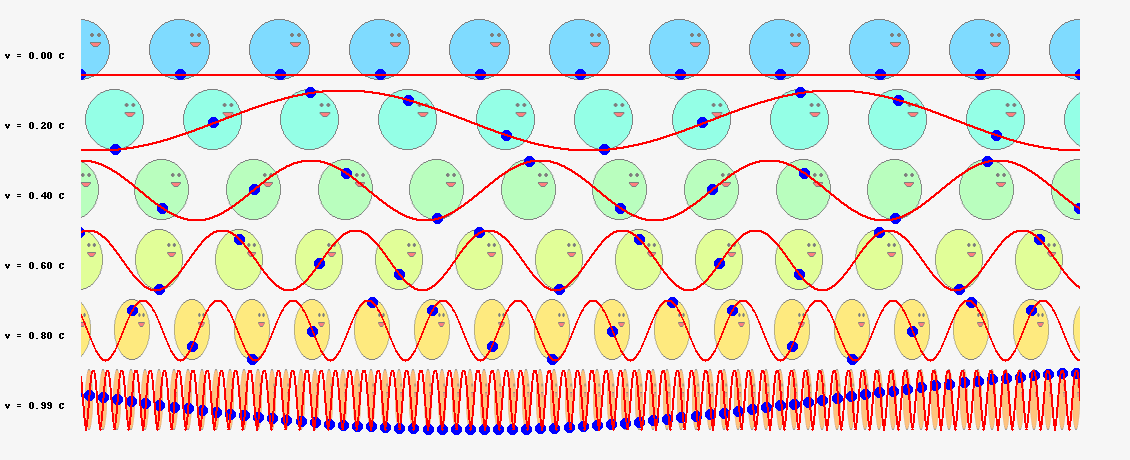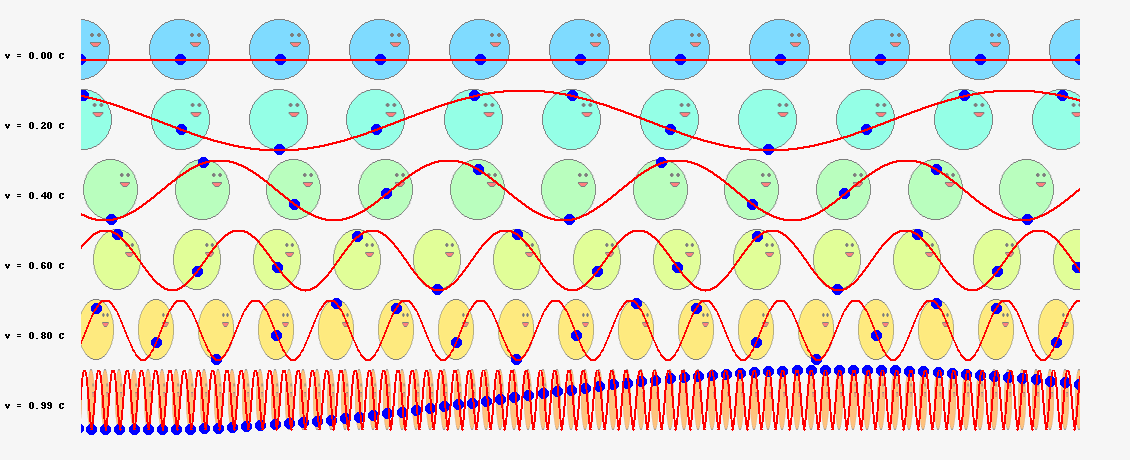
以上の議論を踏まえて、位相一致の法則のアニメーションをブラッシュアップしてみました。今度は粒子内部の振動と位相波を重ねて示し、位相一致の法則が空間のいたるところで成立することがわかるよう、横にたくさん粒子を並べています。
縦に複数の波を並べたのは、速度\(v\)との関係を示すためです。最上段は\(v=0\)、すなわち、\(S^\prime=S\)の特殊ケースです。下段に行くほど、粒子の速度\(v\)が光の速度に近づきます。ローレンツ収縮を意識して、粒子の幅も進行方向に縮めて示しています。粒子の速度\(v\)が大きくなると、赤線で示した位相波の振動数は増えていきますが、位相一致点の青玉の振動は、時間の遅れを反映した、ゆっくりした動きになっていきます。
以上のように、粒子に\(h\nu=mc^2\)で振動数を結び付け、なおかつ、この粒子が速度\(v\)で運動した際のローレンツ変換とも整合する振動現象の描像を得ることができました。
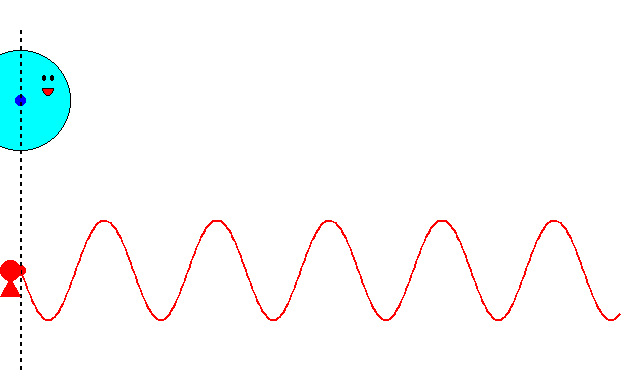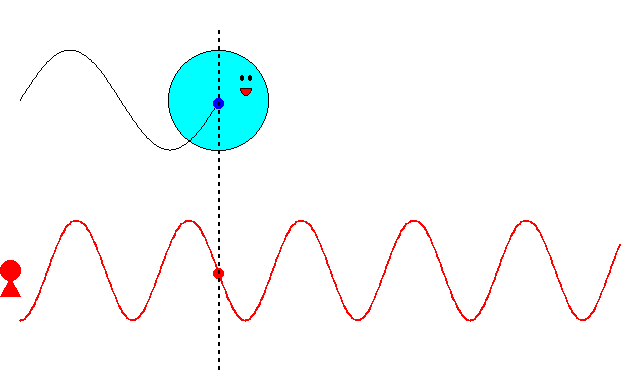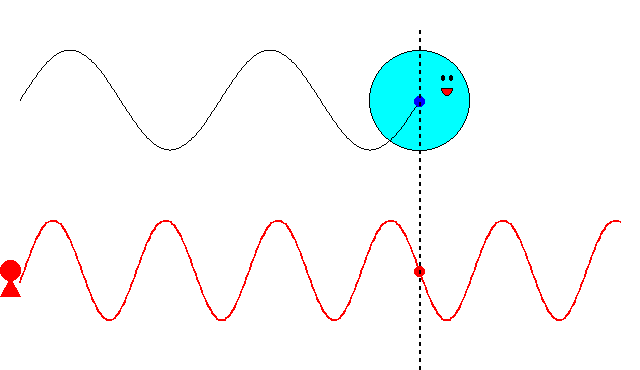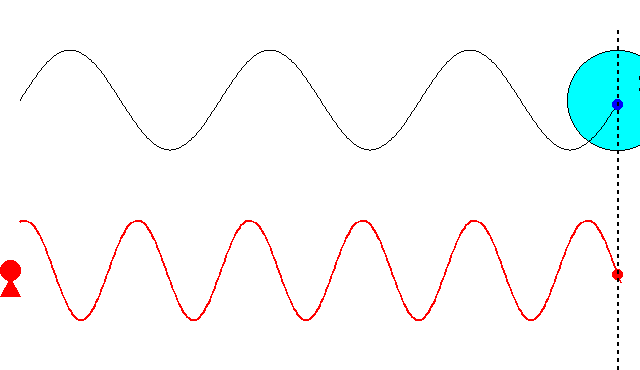
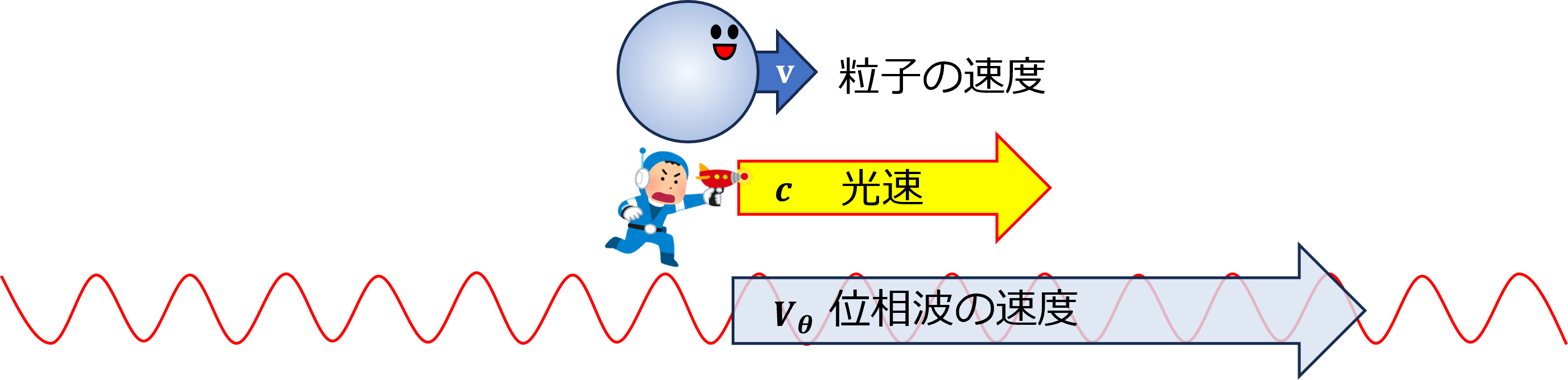
速度\(v\)で運動する粒子との位相一致点は、上のアニメーションで示したとおり、空間上のあらゆる点にとることができます。もし、先に波動が与えられたとして、空間の特定の位置を占めつつ運動する粒子の描像を得るにはどうしたらよいのでしょうか?
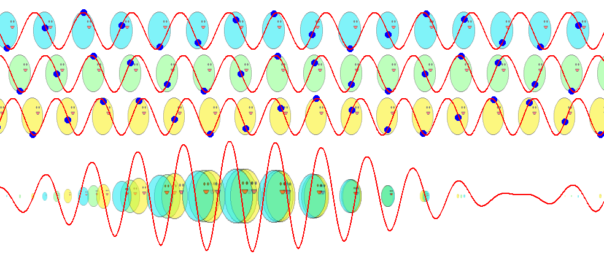
ヒントはすでに、このページの一番上の、アイキャッチ画像に示してあります。次回、いよいよ波束(ウェーブパケット)の群速度と粒子の描像の関係について説明します。