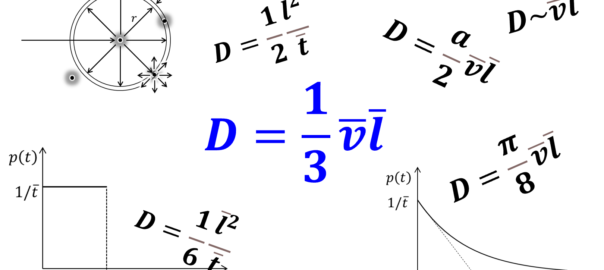渡邉孝信（早稲田大学・電子物理システム学科）

距離\(r\)まで無衝突で進める確率を定式化する

電子が無衝突で進める距離\(r\)の確率も、指数分布に従うと考えられます。今回は、この確率分布を簡単なモデルを使って導出してみましょう。

 

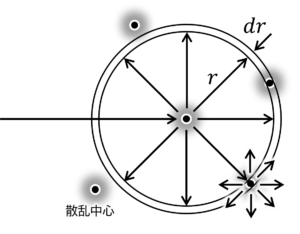
　今、ある電子が、最後に衝突イベントを経験してから、距離\(r\)を無衝突で進んだとし、距離\(r\)と\(r+dr\)の間で次の衝突が起こる確率を考えましょう。この散乱は図7.1に示すように等方的で、衝突後に進む方向は球対称となります。電子の散乱を引き起こす散乱中心の個数密度を\(N_s\)、散乱中心の衝突断面積を\(\sigma\)とおくと、半径\(r\)、厚さ\(dr\)の球殻の体積が\(4\pi r^2dr\)であるので、微小区間\(dr\)の衝突確率は

$$\frac{N_s4\pi r^2 dr\sigma}{4\pi r^2}=N_s\sigma dr\tag{7.1}$$

となります。よって、微小距離\(dr\)を無衝突で進める確率は

$$1-N_s\sigma dr \tag{7.2}$$

です。距離\(r\)を無衝突で進む確率\(p_{\rm free}(r)\)と、距離\(r+dr\)を無衝突で進む確率\(p_{\rm free}(r+dr)\)の間には

$$ p_{\rm free}(r+dr) = p_{\rm free}(r)(1-N_s\sigma)dr\tag{7.3}$$

という関係が成り立つことになります。この式から次の微分方程式

$$ \frac{d p_{\rm free}}{dr}=\frac{p_{\rm free}(r+dr) – p_{\rm free}(r)}{dr}=-N_s\sigma p_{\rm free}(r)\tag{7.4}$$

が導かれるので、一般解を求めると

$$p_{\rm free}(r)=C e^{-N_s\sigma r}\tag{7.5}$$

となります。規格化条件

$$\int_0^\infty p_{\rm free}(r)dr=1\tag{7.6}$$

より、

$$p_{\rm free}(r)=N_s\sigma e^{-N_s\sigma r}\tag{7.7}$$

となります。

　無衝突で進める距離の平均が平均自由行程\(\overline{l}\)なので、

$$\overline{l}=\int_0^\infty rp_{\rm free}(r)dr=\int_0^\infty rN_s\sigma e^{-N_s\sigma r}dr=\frac{1}{N_s\sigma}\tag{7.8}$$

よって、\(p_{\rm free}(r)\)は

$$p_{\rm free}(r)=\frac{1}{\overline{l}}e^{-\frac{r}{\overline{l}}}\tag{7.9}$$

と表されます。

 　ここで少し視点を変えて、今\(r=0\)の位置にある電子が、この先\(r\)まで無衝突で進める確率はどのくらいか？、という問題を考えてみましょう。\(p_{\rm free}(r)dr\)は「\(r\)と\(r+dr\)の区間で初めて次の衝突が起こる確率」を表していますから、距離\(r\)進む間のどこかで衝突が起こる確率は、累積確率

$$\int_0^r p_{\rm free}(r^\prime)dr^\prime\tag{7.10}$$

で表されます。ということは、距離\(r\)進む間に衝突が起きない確率を\(P_{\rm free}(r)\)とすると、

$$P_{\rm free}(r)=1-\int_0^r p_{\rm free}(r^\prime)dr^\prime=e^{-\frac{r}{\overline{l}}}\tag{7.11}$$

と表せることになります。