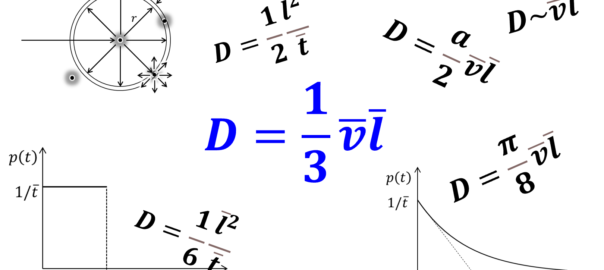渡邉孝信(早稲田大学・電子物理システム学科)
前回の記事で導出した無衝突で進める確率を用いて、第4回の記事で示した拡散係数を定式化しなおしてみましょう。図8.1に示すように、 \(x\)軸方向に電子密度\(n(x)\)が変化している、温度が一様な導体を考えます。今度は、\(x=x_0\)の面に到達する電子の出発位置を限定せず、距離に応じた到達確率を乗じて全区間で積分することによって、拡散流量を求めます。
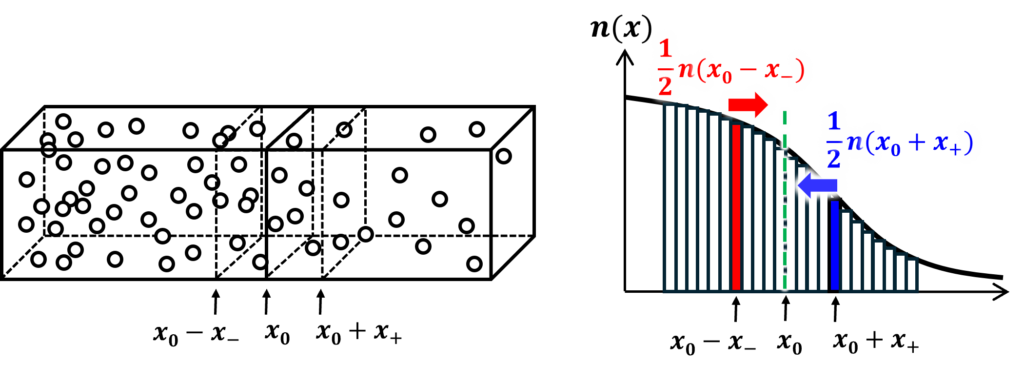
\(x=x_0-x_{-}\)の位置にある電子に注目してみましょう。ここにある電子の1/2が\(+x\)方向を向いているので、平均自由時間\(\overline{t}\)内に\(x=x_0\)の面に到達する可能性がある電子は\(\frac{1}{2}n(x_0-x_{-})dx\)です。これに到達確率\(P_{\rm free}(x_{-})\)を乗じた個数が、無衝突で\(x=x_0\)に到達できます。位置\(x_{-}\)から\(+x\)方向に通過する電子の平均流束を\(f_+(x_{-})dx\)とすると、
$$f_+(x_{-})dx=n(x_0-x_{-})P_{\rm free}(x_{-})\frac{dx}{2\overline{t}}\tag{8.1}$$
と書けます。同様に、位置\(x_{+}\)から\(-x\)方向に通過する電子の平均流束\(f_{-}(x_{+})dx\)は
$$f_-(x_{+})dx=n(x_0+x_{+})P_{\rm free}(x_{+})\frac{dx}{2\overline{t}}\tag{8.2}$$
以上から、\(x=x_0\)における\(+x\)方向への正味の流束\(F_x\)は
$$\begin{eqnarray}F_x &=&\int_0^\infty dx \left \{ f_+(x) – f_{-}(x)\right \}\\&=& \int_0^\infty dxP_{\rm free}(x)\frac{1}{2\overline{t}}\left\{n(x_0-x)-n(x_0+x)\right\}\\&=&-\frac{1}{2\overline{t}}\int_0^\infty dxP_{\rm free}(x)\frac{dn}{dx}\cdot 2x \\&=&-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^\infty x P_{\rm free}(x)dx\label{netflux}\tag{8.3}\end{eqnarray}$$
となります。
ここで、前回求めた到達確率の式
$$P_{\rm free}(x)=e^{-\frac{x}{\overline{l_x}}}\tag{8.4}$$
を式\(\eqref{netflux}\)に代入すると、
$$F_x=-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^\infty x e^{-\frac{x}{\overline{l_x}}}dx=-\frac{\overline{l_x}^2}{\overline{t}}\frac{dn}{dx}=-\overline{v_x}\overline{l_x}\frac{dn}{dx}\tag{8.5}$$
となり、ジィーの本で書かれている拡散係数
$$D=\overline{v_x}\overline{l_x}\tag{8.6}$$
と一致します。3次元なら
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{8.7}$$
です。
あるいはもし、\(P_{\rm free}(x)\)として
$$P_{\rm free}(x)=\left\{\begin{array}{ll}1,&x\leq\overline{l_x}\\0,&x>\overline{l_x}\end{array}\right.\tag{8.8}$$
を仮定すると、
$$F_x=-\frac{1}{\overline{t}}\frac{dn}{dx}\int_0^{\overline{l_x}} x dx=-\frac{\overline{l_x}^2}{2\overline{t}}\frac{dn}{dx}=-\frac{\overline{v_x}\overline{l_x}}{2}\frac{dn}{dx}\tag{8.9}$$
となり、アンダーソンらの本の拡散係数と同様、1/2の係数がつくことになります。3次元なら
$$D=\frac{1}{6}\overline{v}\overline{l}\tag{8.10}$$
です。
以上から、ジィーとアンダーソンの拡散係数の違いが、無衝突距離の確率分布の違いで説明できることがわかりました。適切な式はどちらかと言えば、指数関数の到達確率で導かれる
$$D=\frac{1}{3}\overline{v}\overline{l}\tag{8.7 再掲}$$
の方でしょう。
ここまで詳しく見ていくと、\(D=\overline{v}\overline{l}/3\)という拡散係数の式の導き方にも、いろいろツッコミどころが残ることがわかります。
- 無衝突で進んだ電子のみカウントしているが、衝突したら電子が停止してしまうわけでないのだから、複数回散乱して\(x=x_0\)面に到達する確率も考慮すべきではないか。
- 1回の衝突で過去の運動の履歴が完全に忘却され、次の進行方向が等方的になるという仮定もいかがなものか。
- 「\(x=x_0-x_{-}\)の位置にある電子のうち、右向きの速度を持つ1/2の電子が\(x=x_0\)面に到達する可能性がある」としているが、ほとんどゼロに近い\(v_x\)を持っている電子も結構あるので、1/2は過大評価ではないか。この傾向は\(x=x_0\)から離れるほど顕著になるはずである。
上記の指摘は至極真っ当で、このような問題点を改善しようとした仕事も過去に行われたようですが、満足のいく定式化には至っていないようです。無理に係数を特定せず、パウリの本やランダウ-リフシッツの本のように、係数に曖昧さを明示的に残しておく方が、モヤモヤ感は残りますが、より適切と言えるでしょう。