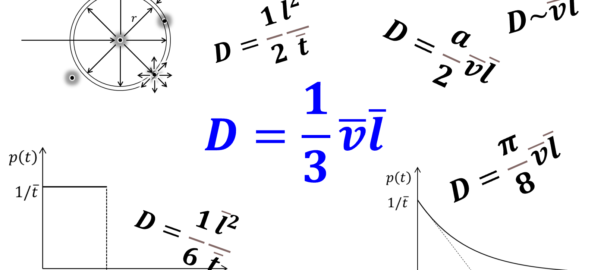渡邉孝信（早稲田大学・電子物理システム学科）

ボルツマン方程式から拡散係数を導く

　非平衡統計力学のボルツマン方程式を学ぶと、ドリフト移動度を定義しなくても、

$$ D= \frac{1}{3}\overline{v}\overline{l}\label{diffusivity3}\tag{3.1}$$

を比較的すっきりと導くことができます。ボルツマン方程式とは、空間座標\(\boldsymbol{r}\)と運動量\(\boldsymbol{p}\)の６次元の位相空間における、粒子系の分布関数\(f(\boldsymbol{r},\boldsymbol{p},t)\)についての微分方程式で、次式で与えられます。

$$ \frac{\partial f}{\partial t}+\frac{\boldsymbol{p}}{m}\cdot\frac{\partial f}{\partial \boldsymbol{r}}+\boldsymbol{F}\cdot\frac{\partial f}{\partial \boldsymbol{p}}=-{\left (\frac{\partial f}{\partial t}\right )}_c\label{boltzmann}\tag{3.2}$$

\(\boldsymbol{F}\)は粒子系に加わる外力、\(-{\left (\frac{\partial f}{\partial t}\right )}_c\)は衝突によって生じる変化、すなわち、微小領域\(d\boldsymbol{rp}d\boldsymbol{p}\)において微小時間\(dt\)に衝突によって生じる\(f\)の変化を表します。この衝突項\(-{\left (\frac{\partial f}{\partial t}\right )}_c\)を

$$ -{\left (\frac{\partial f}{\partial t}\right )}_c=-\frac{f-f_0}{\tau}\tag{3.3}$$

とするのが緩和時間近似です。\(\tau\)が緩和時間と呼ばれるパラメータで、\(f_0\)は熱平衡状態の分布関数を表します。今、外力\(\boldsymbol{F}\)が加わっておらず、濃度の一様な系を仮定すると、式\(\eqref{boltzmann}\)において\(\boldsymbol{F}=\boldsymbol{0}\)、\(\frac{\partial f}{\partial \boldsymbol{r}}=\boldsymbol{0}\)とおけるので、

$$ \frac{d f}{d t}=-\frac{f-f_0}{\tau}\tag{3.4}$$

が解くべき微分方程式となります。初期値\(f(0)\)を境界条件とする解は

$$ f(t)=\left ( f(0) – f_0 \right ) e^{-\frac{t}{\tau}}+f_0\tag{3.5}$$

となり、時定数\(\tau\)で\(f_0\)に落ち着いていく、という解になります。

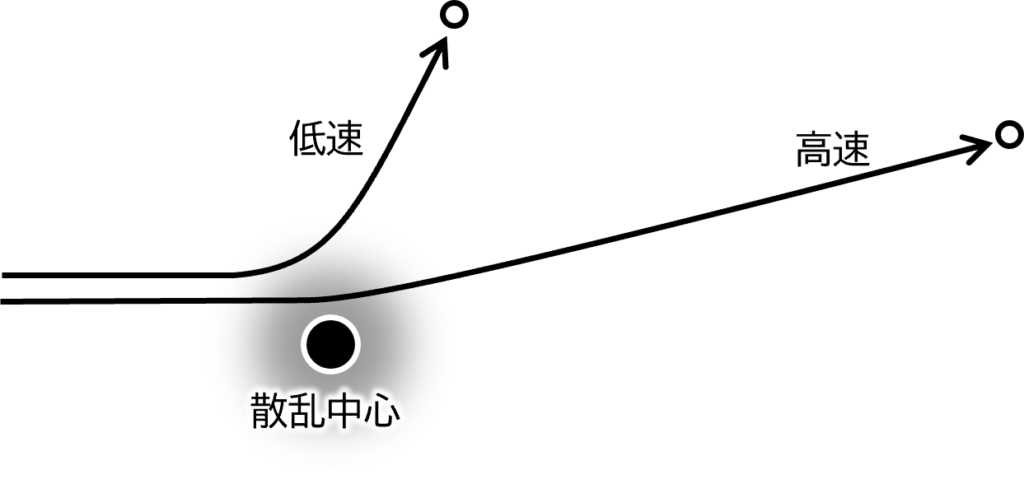
衝突が分布関数に与える影響は、本来、電子の運動エネルギーに依存するはずです。例えば、半導体中の電子が不純物イオンと衝突する場合、電子が速く動いている時はゆっくり動くときと比べて、不純物イオンの周辺のポテンシャルの影響は小さく、正面衝突するのでなければ、進路はそれほど大きく乱されません（図3.1参照)。よって緩和時間\(\tau\)は\(\boldsymbol{p}\)の関数\(\tau(\boldsymbol{p})\)とみなすべきです。それを無視して、緩和時間\(\tau\)を定数とおいてしまおうという、ざっくりした近似を、定緩和時間近似と呼びます。

　拡散電流は、分布関数が実空間上で一様でない場合に生じます。外力\(\boldsymbol{F}\)がなく、濃度が一様でない状態で系が定常状態にあるとき、式\(\eqref{boltzmann}\)において\(\boldsymbol{F}=\boldsymbol{0}\)、\(\frac{\partial f}{\partial t}=0\)とした

$$ \frac{\boldsymbol{p}}{m}\cdot\frac{\partial f}{\partial \boldsymbol{r}}=-\frac{f-f_0}{\tau}\tag{3.6}$$

の解を求めてみましょう。\(\boldsymbol{p}/m=\boldsymbol{v}\)として式変形すると

$$ f(\boldsymbol{r})=f_0(\boldsymbol{r})-\tau\boldsymbol{v}\cdot\frac{\partial f}{\partial\boldsymbol{r} }\label{boltzmann2}\tag{3.7}$$

となります。ここで、\(\tau\boldsymbol{v}\)の大きさが十分小さく、解がべき級数

$$ f=f_0-\tau\boldsymbol{v}\cdot f_1+{(\tau\boldsymbol{v})}^2f_2\cdots\label{perturbation}\tag{3.8}$$

の形で表せると仮定して、\(f_1,f_2,\cdots\)を求めてみます。式\(\eqref{perturbation}\)を式\(\eqref{boltzmann2}\)に代入すると、

$$ f_0-\tau\boldsymbol{v}\cdot f_1+{(\tau\boldsymbol{v})}^2f_2\cdots=f_0-\tau\boldsymbol{v}\cdot\frac{\partial f_0}{\partial \boldsymbol{r}}+{(\tau\boldsymbol{v})}^2\frac{\partial f_1}{\partial \boldsymbol{r}}\tag{3.9}$$

となり、各次の項を比較すると

$$ f_1=\frac{\partial f_0}{\partial \boldsymbol{r}},\;\;\;f_2=\frac{\partial f_1}{\partial \boldsymbol{r}},\cdots$$

と求まります。ここでは展開を１次で打ち切って、

$$ f(\boldsymbol{r})\cong f_0(\boldsymbol{r})-\tau\boldsymbol{v}\cdot\frac{\partial f_0}{\partial\boldsymbol{r} }\tag{3.10}$$

を近似解として採用しましょう。

　拡散電流\(\boldsymbol{J}\)（正確には拡散電流密度。単位はA/cm\({}^2\)）を求めるには、運動量空間で\(\boldsymbol{v}f\)を積分します。

$$ \boldsymbol{J}=-q\int\boldsymbol{v}f d\boldsymbol{p}=-q\int\left\{\boldsymbol{v} f_0 – \tau \boldsymbol{v}\left (\boldsymbol{v}\cdot\frac{\partial f_0}{\partial \boldsymbol{r}} \right) \right\}d\boldsymbol{p}\tag{3.11}$$

今、\(f\)の偏りが実空間の\(x\)方向にのみ一様に生じていると仮定すると、拡散電流は\(x\)成分のみとなり、

$$ J_x=-q\int\left (v_x f_0 – \tau v_x^2 \frac{\partial f_0}{\partial x} \right) d\boldsymbol{p}=-q\tau\overline{v_x^2} \frac{d n}{d x}\tag{3.12}$$

となります。なお、ここでは分布関数が\(f_0(\boldsymbol{r},\boldsymbol{p})=n(\boldsymbol{r})g_0(\boldsymbol{p})\)と変数分離できると仮定し（\(n(\boldsymbol{r})\)は実空間上の電子密度分布を表します）、

$$ \overline{v_x}=\int v_xg_0(\boldsymbol{p})d\boldsymbol{p}=0\tag{3.13}$$

$$ \overline{v_x^2}=\int v_x^2g_0(\boldsymbol{p})d\boldsymbol{p}\left (=\frac{k_BT}{m}\right )\tag{3.14}$$

としています。\( \overline{v_x^2}= \overline{v^2}/3\)とおけるので

$$ J_x=-q\frac{\tau\overline{v^2}}{3}\frac{d n}{d x}\tag{3.15}$$

となり、これをフィックの法則

$$ J_x=-qD\frac{d n}{d x}\tag{3.16}$$

と比較すると、拡散係数\(D\)は

$$ D=\frac{1}{3}\tau\overline{v^2}\label{diffusivity4}\tag{3.17}$$

となります。緩和時間\(\tau\)を平均自由時間\(\overline{t}\)、根二乗平均速度\(\sqrt{\overline{v^2}}\)を平均熱速度\(\overline{v}\)とみなせば、\(\overline{l}=\overline{v}\overline{t}\)とおくことで、式\(\eqref{diffusivity4}\)は式\(\eqref{diffusivity3}\)と一致します。緩和時間\(\tau\)と平均自由時間\(\overline{t}\)は元来異なる概念ですが、１回の衝突で過去の履歴が完全に失われ速度分布がリセットされると仮定すると、両者は一致します（この仮定はよく設けられる仮定ですが、よくよく考えると、必ずしも妥当とは言い切れない仮定です）。

　念のため断っておきますが、「\(D=\overline{v}\overline{l}/3\) が正しい」と言いたいのではありません。ボルツマン方程式の定緩和時間近似で導かれる拡散係数と整合する、と言いたいだけです。

渡邉孝信（早稲田大学・電子物理システム学科）

ドリフト移動度から拡散係数を決めてみる

ドリフト移動度\(\mu\)は、 \(q\)を素電荷、\(m\)を電子の質量（正確に言うと有効質量）、\(\overline{t}\)を平均自由時間として

$$\mu=\frac{q\overline{t}}{m} \tag{2.1}$$

と表されます。\(\mu=q\overline{t}/(2m)\)としていた本も以前にあったようですが、それは誤りだというのが現在の大方の見解です。

これはアシュクロフト-マーミン著「固体物理学の基礎」にも書かれている有名な話なのですが、1900年に最初に電気伝導の古典的理論を発表したドルーデ自身、論文で\(\mu=q\overline{t}/(2m)\)と書いていました。その後、1905年に発表されたローレンツの論文で\(\mu=q\overline{t}/m\)に修正されたのです。

ドリフト移動度\(\mu\)に1/2をつけるか否かという問題はたいへん微妙で、アシュクロフト-マーミンの本でも第１章の最初の演習問題として取り上げて読者に熟考を促しています。実はこの問題が、ドリフト移動度だけでなく、拡散係数の式の違いにも関係してくる、というのがこのシリーズ記事を通して伝えたいことなのですが、この件については追々詳しく説明していきます。

　さて、ドリフト移動度\(\mu\)が決まっているなら、アインシュタインの関係式から

$$D=\frac{\mu}{q}k_BT=\frac{\overline{t}}{m}k_BT \tag{2.2}$$

と拡散係数\(D\)が一意に決まります。系が熱平衡状態に近く、エネルギーの等分配則

$$\frac{1}{2}m\overline{v^2}=\frac{3}{2}k_BT \label{equipartition}\tag{2.3}$$

が成り立つと考えてよければ、平均熱速度を根二乗平均速度として（\(\overline{v}=\sqrt{\overline{v^2}}\)）

$$D=\frac{1}{3}\overline{v^2}\overline{t}=\frac{1}{3}\overline{v}\overline{l}=\frac{\overline{l}^2}{3\overline{t}} \label{diffusivity}\tag{2.4}$$

となります。ここで\(\overline{l}=\overline{v}\overline{t}\)としました。

　ここで注意すべきことは、熱平衡状態で成り立つエネルギーの等分配則の式\(\eqref{equipartition}\)を仮定している点です。拡散電流が流れているときは熱平衡状態ではありませんから、マクスウェル・ボルツマン分布は歪んでいるはずで、等分配則も厳密には成り立ちません。式\(\eqref{diffusivity}\)はあくまで近似式に過ぎないことを忘れないようにしましょう。

渡邉孝信（早稲田大学・電子物理システム学科）

ねぇおかしいでしょ1/2

半導体デバイスの授業では、キャリアの基本的な輸送機構として、

ドリフト電流　と　拡散電流

の概念をまず学びます。まだ非平衡統計力学を学んでいない場合がほとんどでしょうから、ドリフトや拡散の概念を説明する際は、高校物理で登場する気体分子運動論が用いられます。熱運動する気体分子に電子をなぞらえ、平均速度 \(\overline{v}\) 、平均自由行程 \(\overline{l}\) 、平均自由時間\(\overline{t}\) を使って、ドリフト移動度 \(\mu\) と拡散係数 \(D\) を表してみせるのです。

　その際に困るのは、この初歩的に導出される拡散係数 \(D\) の式が本によってまちまちで、しかもイマイチ釈然としない説明が多いことです。一方、ドリフト移動度 \(\mu\) の式はほぼ１通りに落ち着いています。そこで、金科玉条のアインシュタインの関係式

$$ D=\frac{\mu}{q}k_BT \label{einstein}\tag{1.1}$$

を使って（ \(q\)は素電荷、 \(k_B\)はボルツマン定数、 \(T\)は絶対温度）、ドリフト移動度 \(\mu\) から拡散係数\(D\) を決定することで、そうした混乱を回避している教科書も多数あります。というよりむしろ、拡散係数\(D\) は式\(\eqref{einstein}\)で定めるべきでしょう。

　そうは言っても、拡散というキャリア輸送の微視的描像をつかむには、気体分子運動論に基づく説明に触れておくこともたいへん重要です。

　表１に、筆者が知っている範囲ですが、代表的な教科書や専門書に書かれている拡散係数の式をまとめておきました。どうしてこうもいろいろあるのでしょうか？

それは、平均速度 \(\overline{v}\) 、平均自由行程 \(\overline{l}\)、平均自由時間 \(\overline{t}\)といった量の「平均」の取り方に、いろいろな方法や考え方があるからです。

表１　様々な拡散係数の式。 \(\overline{v}\) :平均速度（熱運動速度）、 \(\overline{l}\)：平均自由行程、\(\overline{t}\)：平均自由時間 

まず注意すべきは、考えている系の次元が必ずしも同じではないということです。３次元空間における拡散流を考える際、その流れの方向に対して斜影をとるため、\(\overline{v}\)と\(\overline{l}\)はそれぞれ\(1/\sqrt{3}\)倍されます。３次元モデルの多くに1/3や1/6という係数がついているのはそのためです。終始１次元で議論している本では、1/3倍しないままにしています。

また、平均熱速度 には「速さの平均」や「根二乗平均速度」など、複数の定義があることも念頭に置いておく必要があります。ただしこの差はそれほど大きくありません。マクスウェル－ボルツマン分布を仮定した場合

$$平均速さ： \overline{|\boldsymbol{v}|}=\sqrt{\frac{8k_BT}{\pi m}} \label{meanvelocity}\tag{1.2}$$

$$根二乗平均速度： \sqrt{\overline{\boldsymbol{v}^2}}=\sqrt{\frac{3k_BT}{m}} \label{rmsvelocity}\tag{1.3}$$

となり、根二乗平均速度は速さの平均の0.92倍と、若干ですが小さめになります。

表1の文献[9]のMeyerの本は、気体分子運動論に基づいて拡散係数を定式化した最初期の仕事です。Meyerの式では、式\(\eqref{meanvelocity}\)の速さの平均\(\overline{|\boldsymbol{v}|}\)が\(\overline{v}\)として採用されていて、平均自由行程も\(\overline{l}=\overline{|\boldsymbol{v}|}\overline{t}\)とおいています。これらを根二乗平均速度\(\sqrt{\overline{\boldsymbol{v}^2}}\)に置き換えると、\(\overline{|\boldsymbol{v}|}=\sqrt{8/(3\pi)}\sqrt{\overline{\boldsymbol{v}^2}}\)、\(\overline{l}=\sqrt{8/(3\pi)}\sqrt{\overline{\boldsymbol{v}^2}}\overline{t}\)となるので、

$$D=\frac{\pi}{8}\overline{v}\overline{l}=\frac{\pi}{8}\overline{|\boldsymbol{v}|}^2\overline{t}=\frac{\pi}{8}\frac{8}{3\pi}\overline{\boldsymbol{v}^2}\overline{t}=\frac{1}{3}\overline{{\boldsymbol{v}}^2}\overline{t}$$

となり、\(D=\overline{v}\overline{l}/3\)としている他の文献と一致します。

　もう一つ、拡散係数\(D\)の違いの要因となっているのは、平均自由時間\(\overline{t}\)と平均自由行程\(\overline{l}\)の「平均」の取り方です。1/2倍の係数がかかったりかからなかったりするのは、この平均操作の仕方の違いに起因します（注：パウリ[3]とChapman[11]はまた別の理由で1/2の係数をつけています）。気体分子運動論では、気体分子同士の衝突イベントと次の衝突イベントの間の時間の平均が\(\overline{t}\)、衝突イベントから次の衝突イベントが起きるまでに進める距離の平均を\(\overline{l}\)、としています。これらの統計平均を計算する際、どのような確率分布を仮定するかによって、平均値（期待値）が変わってしまうのです。このシリーズ記事では、この確率分布の取り扱い方に焦点を当てて、拡散係数の式の違いを議論していきます。