博士後期課程3年生のSylvia Y. Y. Chungさんが、3月26日、早稲田アリーナで開催された学位授与式で博士学位記を授与されました。

博士後期課程3年生のSylvia Y. Y. Chungさんが、3月26日、早稲田アリーナで開催された学位授与式で博士学位記を授与されました。

2022年1月29日~30日に開催された「電子デバイス界面テクノロジー研究会」(第27回)で、博士後期課程3年のSylvia Y. Y. Chungさんが「Identifying an Anomalous Phonon Mode in SiGe Alloy using Molecular Dynamics Simulation」と題して口頭発表行い、この発表で服部賞(若手講演奨励賞 評価・解析部門)を受賞しました。
Sylvia Y. Y. Chungさん(博士後期課程3年生)と富田基裕さん(次席研究員)が、2021年7月2日~3日にオンライン開催された第5回フォノンエンジニアリング研究会で発表し、Sylviaさんが講演奨励賞、富田さんが優秀ポスター賞を受賞しました。
Deal-Groveモデルでは、SiO2膜厚が薄い初期の段階は界面における酸化反応が律速となり、そのためSiO2膜厚は時間に対して線形に増加すると説明されてきました。しかし2004~2005年にかけて発表された第一原理量子化学計算[1,2]により、
界面におけるO2分子とSi基板の化学反応にはエネルギー障壁がほぼ存在しない
という驚くべき事実が明らかにされました。
では初期の線形領域はなぜ存在するのでしょうか? 線形領域の酸化速度の活性化エネルギー2.0eVは、いったい何のエネルギー障壁を示しているのでしょうか?
上記の界面反応の量子化学計算を発表したBongiornoとPasquarello[1]は、界面近傍のSiO2層は圧縮歪みを帯びており、O2分子の拡散障壁が1.24eVから2.0eVに上がっているのだ、と主張しました。界面から約1nmの範囲のSiO2層は構造遷移領域と呼ばれ、この領域で密度が増加していることが以前より実験でも指摘されていました。
だとすると、Deal-Grove方程式の界面反応速度係数\(k\)も、SiO2膜厚が薄い初期段階のO2分子の拡散速度に関係していることになります。\(k\)が拡散係数\(D_0\)に関係しているとしたら、初期の異常な酸化速度の解釈も変わる可能性があります。
そこで筆者(渡邉)[3]は、界面近傍の構造遷移領域で局所的に拡散障壁が増加するというモデルを前提にして、Deal-Grove方程式に代わる新しい線形‐放物型方程式を導き、線形速度定数\(B/A\)を新たに定式化しました。新しい方程式を使って、線形速度定数\(B/A\)の実験値に合うような構造遷移領域の厚さを求めたところ、その厚さはおおむね1nm程度と算出されました。これは実験で指摘されていた構造遷移領域の厚さと一致します。そして予想通り、初期の異常な酸化速度も拡散速度の上昇で説明すべきであることが判明し、Fargeixらの解析[4]以来お蔵入りにされてきた「初期増速拡散説」が復活することがわかりました。
[1] A. Bongiorno, A. Pasquarello, Phys. Rev. Lett., 93, 086102 (2004).
[2] T. Akiyama and H. Kageshima, Surf. Sci., 576, L65 (2005).
[3] T. Watanabe, K. Tatsumura, I. Ohdomari, Phys. Rev. Lett., 96, 196102 (2006).
[4] A. Fargeix, G. Ghibaudo, G. Kamarinos, J. Appl. Phys. 54, 2878 (1983).
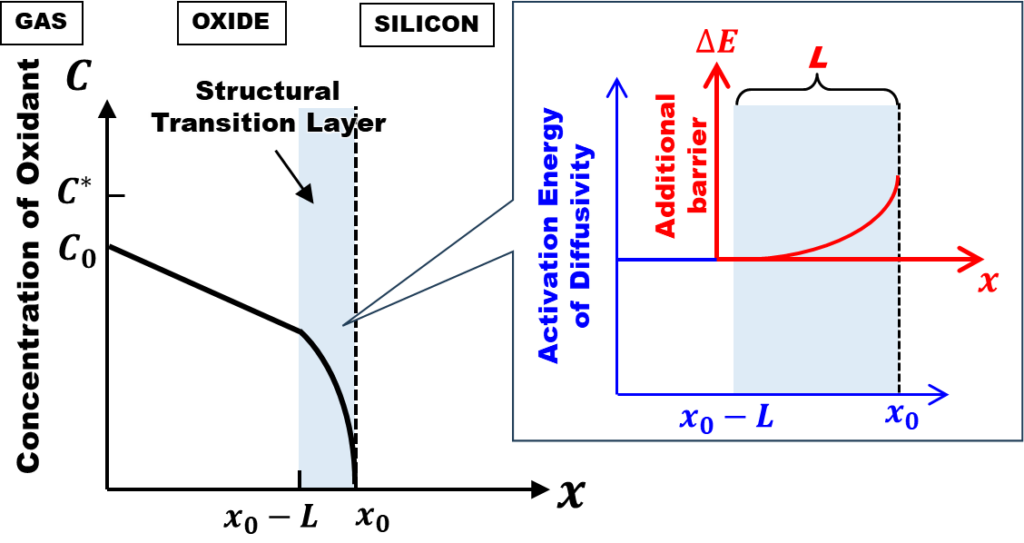
上図が、完全拡散律速熱モデルで想定するO2濃度プロファイルです。右側のグラフは、構造遷移領域におけるO2分子の拡散係数の活性化エネルギーの分布を示しています。Deal-Groveのような界面反応の障壁の代わりに、界面近傍の厚さLの構造遷移領域内で拡散障壁が上昇し、濃度が急低下していると考えるのです。
次回から、上図のモデルに基づく新しい酸化速度方程式の導出を示していきます。
ドライ酸化のごく初期で見られる酸化速度の異常な増加は、当初、酸化種が速く拡散するために起こる現象と考えられていました。前回紹介したように、DealとGroveは、Mott-Cabreraのモデルを引き合いに出してイオン化した酸化種の増速拡散で説明しています。
しかし、1983年に発表されたFargeixらの解析1)で、この増速拡散モデルは否定されることになります。今回はFargeixらがどんな解析を行ったのか紹介いたします。
Fargeixらは、酸化速度の逆数\(dt/dx_0\)の振る舞いを調べました。Deal-Groveの微分方程式によると、\(dt/dx_0\)は
$$ \frac{dt}{dX_0}=\frac{A}{B}+\frac{2}{B}x_0 $$
と与えられ、傾きが\(2/B\)、切片が\(A/B\)の直線を描きます。しかしドライ酸化では、下図に示すように酸化膜厚\(x_0\)が薄い初期の領域で直線ではなくカーブを描きます。このカーブを描いている部分が初期の異常領域です。注目すべきは、酸化条件によらずこのカーブが常に下に曲がっていること、すなわち、\(x_0\)が小さくなるほどグラフの傾きが大きくなるという共通点があることです。
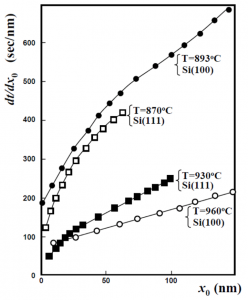
酸化膜の成長速度の逆数と酸化膜厚の関係。初期領域でグラフが下に曲がっている。(Fargeixらの論文1)を元に作成)
この実験結果から以下のことが言えます。\(x_0\)が小さくなるにつれてグラフが下に曲がっているということは、Deal-Grove方程式によると
のいずれか、ということになります。
もし酸化種の増速拡散が原因でグラフが曲がったとするなら、拡散係数\(D_0\)に比例して\(B\)も大きくなるはずです。よって、下図に示すように傾き\(2/B\)は減少し、グラフは上向きに曲がることになります。これはFargeixらの実験結果と逆の傾向です。
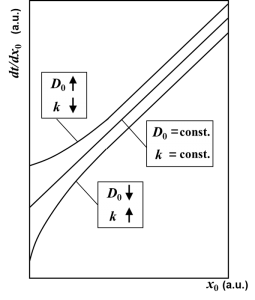
Deal-Groveモデルに基づくグラフの曲がりの解釈。初期領域で拡散係数D0が増加しているとするとグラフが上に曲がらなければならない。
Fargeixらの実験結果を説明するには。界面反応速度定数\(k\)が\(x_0\rightarrow 0\)で増加し、線形速度定数\(B/A\)の逆数である切片\(A/B\)が低下していると考えなければなりません。
こうして、ドライ酸化の初期にみられる線形特性からのズレは、界面における酸化反応速度が速くなっているからだとされ、DealとGroveが言うような酸化種の増速拡散によるものではない、という結論に至ったのです。
ただしFargeixが導いた結論は、あくまでDeal-Grove方程式に基づく解釈です。2006年に筆者(渡邉)が発表した新しい線形-放物型方程式2)ではFargeixらの実験の解釈が180度変わり、「初期増速拡散」説が復活することがわかりました。次回からこの新しいモデルを解説していきます。
前回まで、仕訳の仕方、試算表および財務諸表の簡易版であるサマリー表の作り方を一通り見てきました。次に、これら帳簿の運用方法を説明します。
4月に交付額が決まったら、まずは空の帳簿を作成し、最初の取引として仕訳帳に交付金の入金を記録します。実際の入金は数か月先になる場合が多いですが、所属機関で研究費の執行が可能になっていれば、研究者から見れば入金されたも同然です。入金扱いで問題ありません。
次に、年間の支出計画を引当金に計上します。できるだけ確実性が高い支出計画を記載し、本当に支出するかどうか読めない支出計画は、優先度が高くなければ記載しないことを勧めます。後々の計画変更をできるかぎり抑制し、純資産の見積もりの精度を高めるためです。
年度の初頭に予算計画を立てたら、あとは経理担当者に仕訳帳への記入を任せます。月に一度くらいのペースでミーティングを行い、引当金の中身を精査していけば十分でしょう。
ただし、サマリー表は、仕訳帳、試算表と連動させてプロジェクトリーダーが常時見られるようにしておきます。帳簿ファイルをクラウド・サーバーに保存して共有しておくと良いでしょう。プロジェクトのメンバーから日々寄せられる買い物要求に対して可否を判断するには、純資産の正確な金額を常に把握しておく必要があるからです。
引当金は月毎に分けていますので、過去の月の引当金はゼロ円になるのが理想的です。もし、4月に利用した実験施設の使用料の請求書が5月に発行されると判明した場合、「引当金(4月)」に計上していた金額をいったん取り下げ、改めて「引当金(5月)」に計上しなおす習慣にしておけば、過去の月の引当金はゼロ円になるはずです。ゼロ円にならなければどこかに問題があるはずなので、この作業を通じて様々なミス、トラブルを発見することができます。
既に述べたように、ここでは総勘定元帳への転記を省略していますが、引当金のチェック用に、引当金の勘定元帳くらいは月に一度作成しても良いかもしれません。ただし、EXCELのフィルタ機能を使えば仕訳帳の中で引当金の項目を抽出できますので、わざわざ勘定元帳を作成しなくても問題なく作業はできるでしょう。
この記事では、複式簿記の仕組みをつかって、年度予算の適切な執行を補助する方法を解説してきました。作業のゴールは表3のサマリー表の作成ですが、これを作成するだけなら、なにも複式簿記にする必要はありません。従来の支出管理表に加えて、執行予定の金額と執行予定時期を記録した帳簿を作っておけば、全く同じ表が作成できるからです。
それでも複式簿記を勧める理由は、簿記の基本的な知識がある人になら誰にでも日々の帳簿への記入作業を任せられるというメリットがあるからです。簿記の勉強を兼ねて学生に協力してもらうのも有意義でしょう。仕訳のルールさえ理解してもらえていれば、経理担当者の引継ぎがスムーズに行えますし、複数人で共同管理することも可能です。ローカル・ルールではなく、標準化された枠組みの中で所望の機能を実現しているところに、ここで紹介した方法の良さがあると思います。
(渡邉 孝信)
「サマリー表」とは、研究費の経理処理に必要な情報をまとめた、財務諸表の簡易版です。バランスシートの「資産」「負債」「純資産」の金額、損益計算書の中の「費用」の内訳、そして各月の「引当金」の残高を一覧表示させます。
表2に示した試算表から作成したサマリー表を表3に示します。これを「科研費・基盤研究(〇)」、「○○財団研究助成金」など研究費ごとに用意します。いちいち新たに作成するのではなく、試算表と連動して自動的に更新されるように、同じEXCELファイル内に作り込んでおきます。

1行目の右の方に、「資産」および「負債」の合計金額が記載されています。これは「試算表」の「資産」および「負債」の勘定科目の、「当期増分」の合計金額です。2行目の右端にある「純資産」は、「資産」から「負債」を引いた差分です。この「資産」、「負債」、「純資産」の3つの金額からなる極めて単純な表が「バランスシート」になっています。「純資産」は、現在の研究費の残金のうち、支出予定が決まっていない金額、すなわち、これから自由に使途を決められる研究費の余裕を表しています。この例では、この時点で73万円ほど余裕があることになります。年度初めに純資産が沢山あると安心ですが、年度末に向けてゼロになるように執行のペースを調節していく必要があります。
3行目以降は、「試算表」のうち、「費用」と「負債」の内訳を見やすく並べ替えたものです。公的研究費の場合、「設備備品費」、「消耗品費」、・・・といった費目の額が交付時に決まっています。ある程度の費目間流用は認められているものの、基本的には計画通り執行することが求められますので、各費目の合計金額が許容範囲に収まっているどうかもチェックする必要があります。そこで、「予算額」という列に、交付時に設定した各費目の金額を参考データとして記載しています。
なお、表3の例では国内旅費が予算オーバーになっていますが、科研費の場合、直接経費総額の50%までは費目間流用が認められているので問題ありません(科研費ハンドブック2018年度版参照)。 さらに付け加えると、直接経費総額の50% が300万円以下の場合は、300万円まで費目間流用が認められています。ですので、年度予算が数百万円規模の科研費の場合、費目間流用制限で困ることはほとんどありません。科研費は柔軟でとても良い制度です。
3行目以降の右の方に、各月の「引当金」に計上した金額が記載されています。これが現時点で予定されている未執行の金額を表しています。過去の月の引当金がゼロになっていない場合は要注意です。なぜなら、その月に予定していた支出が完了していないことを意味しているからです。単に請求書が手元に届いていないだけかもしれないし、業者に発注するように指示していたのに当の担当者が忘れていた、といったミスが潜んでいるかもしれません。あるいは、支出計画から外したつもりでいたのに、経理担当者に正しく伝達されておらず、帳簿に反映されていなかっただけかもしれません。
このように、「引当金」の数字は、研究費執行上の様々なトラブルを発見するトリガーとして大変役立ちます。
これまでの記事で、仕訳の仕方、試算表およびサマリー表の作り方まで一通り見てきました。次回は、これら帳簿の日々の運用方法を説明します。
(渡邉 孝信)
企業会計では、各期末に
という作業をします。これに対し研究費の執行では、年度途中の好きな時にいつでも財務諸表を閲覧できるようにしなければなりません。期末になってから財務諸表を作っても、バランスシートの中身がすべてゼロ円になってしまっていて全く意味がありません。 そこで、上記の一連の作業を自動化し、期中における最新の財務諸表をリアルタイムで見えるようにする必要があります。
研究費の管理にEXCELを使っている方が多いと思いますが、EXCELで複式簿記を行う場合に厄介な作業が「勘定元帳への転記」です。これを自動化するにはどうしてもEXCELマクロ(VBA)の助けが必要となり、一気にハードルが高くなってしまいます。
研究費の管理程度の業務ならば、勘定元帳は必要ありません。ここでは勘定元帳への転記の手続きをスキップし、仕訳帳から直接、各勘定科目の残高を記載した試算表を作成するやり方を勧めます。
表2に試算表を示します。勘定科目ごとに、仕訳帳の借方に記載された金額の合計と、貸方に記載された金額の合計が記載されています。EXCELのSUMIF関数を使えば、仕訳帳の借方、貸方の列から該当する勘定科目の金額を探して合計できるので、仕訳帳と連動させて常に最新の試算表を表示することができます。
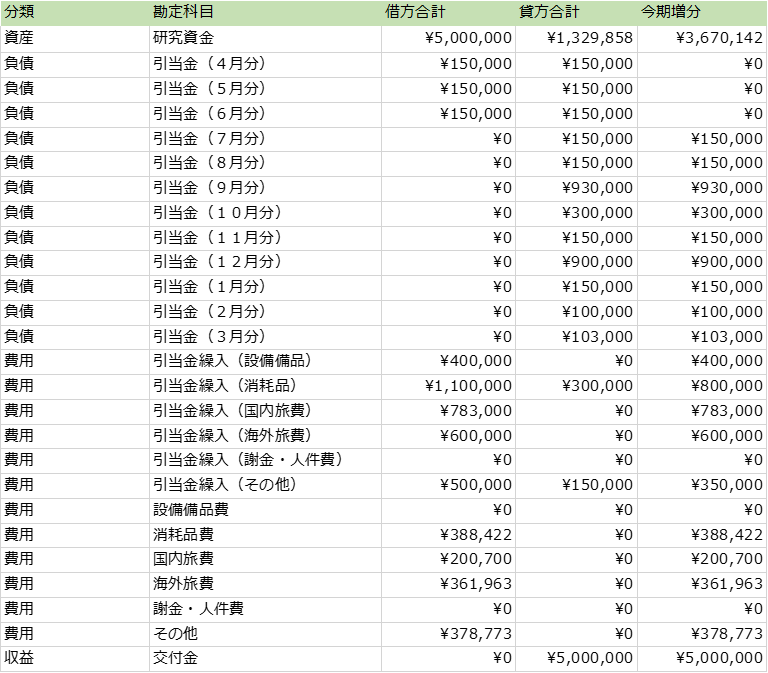
例えば勘定科目「研究資金」の「借方合計」のセルには
=SUMIF(I:I,B2,J:J)
と記入します。試算表の右側に仕訳帳があり、I列は仕訳帳の借方勘定科目の列、J列は借方の金額が並んでいる列です。B列は試算表の中の勘定科目を指します。
同様に 勘定科目「研究資金」の「借方合計」のセルには
=SUMIF(K:K,B2,L:L)
と記入します。K列は仕訳帳の貸方勘定科目の列、L列は貸方の金額が並んでいる列です。
一番右端の「当期増分」は借方合計金額と貸方合計金額の差分ですが、勘定科目のポジションによって差分の取り方に違いがありますので注意が必要です。
「資産」および「費用」に分類される勘定科目の場合は、
当期増分 = 借方合計 ー 貸方合計
と計算します。「負債」および「収益」に分類される勘定科目の場合は
当期増分 = 貸方合計 ー 借方合計
で計算します。EXCELの関数で実現するなら、例えば勘定科目「研究資金」の「当期増分」のセルに
=IF(OR(A2=”資産”,A2=”費用”),C2-D2,D2-C2)
と記入します。
プラスの金額になるようにこのように場合分けするのですが、マイナスの数字になるケースもないとは限りませんので、安易に差分の絶対値を取らないようにしてください。
試算表ができてしまえば、研究費の執行状況の全容が見えてきます。例えば、交付金500万円のうち、1,329,858円が既に消費され、当初立てた支出計画が6月分まで順調に執行されている、といったことがこの表からうかがえます。
ここからさらに必要な情報を整理してまとめた、財務諸表の簡易バージョン「サマリー表」の作り方の例を次回紹介します。
(渡邉 孝信)
研究費管理用の勘定科目の例を示します。ポイントは「引当金」と「引当金繰入」にあります。この2種類の勘定科目を使って、いつごろ、どの費目の支出を予定しているかを明示します。
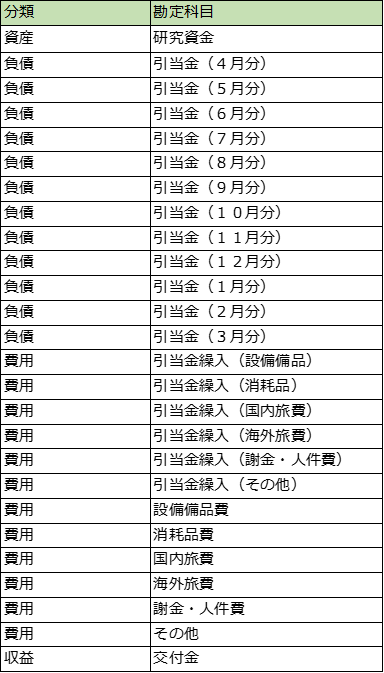
「引当金」は、4月分から翌年の3月分まで、月毎に分かれています。これで、何月にいくら、執行すべき予定があるかがわかります。引当金に計上する際は、相手方勘定科目に「引当金繰入」を指定します。「引当金繰入」は、「設備備品費」、「消耗品費」、・・・のように研究費の費目ごとにわかれているので、どの費目の支出が予定されているかを把握できます。
帳簿は研究費の種類ごとに用意します。ここで言う研究費の種類とは、例えば「科研費・基盤研究(〇)」とか「○○財団研究助成金」などを指します。EXCELを使うなら別々のシートで各研究費を管理します。全てを一つにまとめることもできますが、その場合、上の表に示した勘定科目のうち、「交付金」を除くすべての勘定科目を研究費の種類の数だけ用意しなければならず、かえって仕訳が面倒になります。
次回は、この勘定科目を使った仕訳の方法を具体例を示しながら解説します。
(渡邉 孝信)
Deal-Groveの線形-放物型成長曲線
$$x_0^2+Ax_0 =B (t+\tau) $$
は、ウェット酸化についてはほぼ\(\tau=0\)となり、\(t=0\)、\(x_0=0\)の初期段階からDeal-Groveモデルで記述できます。しかし、ドライ酸化に関しては\(\tau\neq 0\)であり、\(t=0\)付近の初期段階は線形-放物型成長曲線から外れてしまいます。ドライ酸化において、初期酸化はDeal-Groveモデルよりもかなり速く進みます。
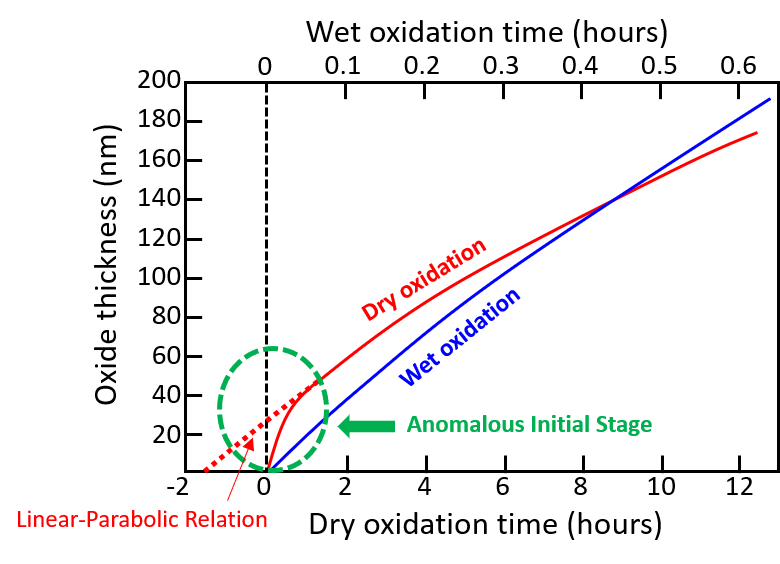
ドライ酸化とウェット酸化における極初期のSiO2膜成長曲線 。ウェット酸化はSiO2膜厚ゼロからDeal-Grove方程式に従うが、ドライ酸化は膜厚40nm程度まで成長速度がDeal-Grove方程式の解より著しく増大する。
ドライ酸化に見られるこの初期の速い酸化は、実はそれほど珍しい現象ではなく、CuやAlなど金属表面の酸化でも観測されていました。金属表面でみられる初期の速い酸化現象を最初に説明したのがMottです。その後Mottは、Cabreraと一緒に、金属表面の酸化膜の成長速度を体系的に説明した論文1)にまとめあげました。これが後に頻繁に引用され、Mott-Cabreraモデルと呼ばれるようになりました。
CuやAlの表面の酸化では、金属がイオン化して酸化膜中を拡散し、表面でイオン化した酸素イオンと出会って酸化反応を起こすと考えられています。これら個々のイオンが作る電界はデバイ遮蔽のメカニズムで打ち消されますが、デバイ長以下の近距離では無視できない電界が残ります。
Mott-Cabreraモデルによると、金属酸化膜の厚さがデバイ長以下の場合は、酸化膜表面でイオン化した酸素分子がつくる電界が酸化膜の膜厚方向全体に及びます。この電界によって酸化膜中の金属イオンの動きが加速され、初期の酸化速度が著しく増加すると説明されます。
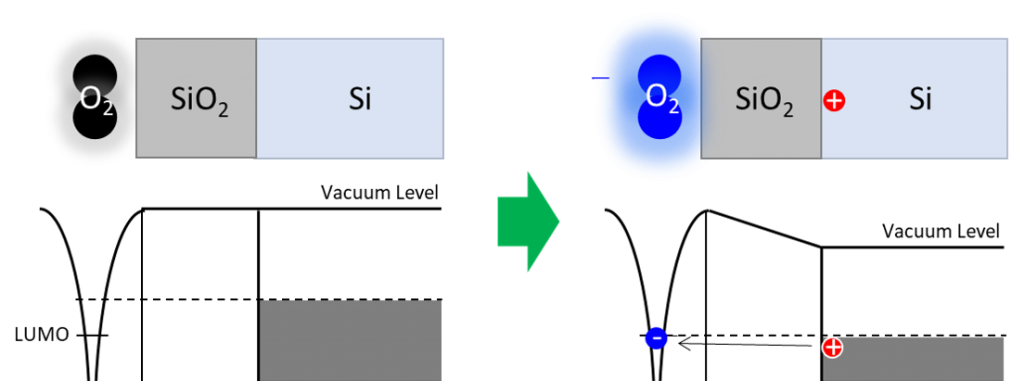
Mott-Cabreraの初期酸化モデル。表面に吸着した酸素分子がイオン化し、薄い酸化膜中に形成された電界によってイオンの拡散が促進される。
Si表面の熱酸化ではSiは動かず、酸化種分子だけが酸化膜を拡散すると考えられていますので、DealとGroveは、イオン化した酸化種の拡散がこの電界で促進されているだろうと考察しました。
DealとGroveの見積もりによると、酸化膜表面に吸着したO2分子が電離してできるプラズマのデバイ長は1000℃で15nm程度となり、初期の異常な酸化速度が観測される領域とオーダーで一致します。一方H2O分子の場合は0.6nmしかなく、ウェット酸化で初期異常が観測されないのはこのためであろうと考察しました。
なかなか見事な説明です。しかし、このイオン化した酸化種の拡散が増速しているという解釈は、1983年にFargeixらが行った解析により2)否定されることになります。