Deal-Groveモデルでは、SiO2膜厚が薄い初期の段階は界面における酸化反応が律速となり、そのためSiO2膜厚は時間に対して線形に増加すると説明されてきました。しかし2004~2005年にかけて発表された第一原理量子化学計算[1,2]により、
界面におけるO2分子とSi基板の化学反応にはエネルギー障壁がほぼ存在しない
という驚くべき事実が明らかにされました。
では初期の線形領域はなぜ存在するのでしょうか? 線形領域の酸化速度の活性化エネルギー2.0eVは、いったい何のエネルギー障壁を示しているのでしょうか?
上記の界面反応の量子化学計算を発表したBongiornoとPasquarello[1]は、界面近傍のSiO2層は圧縮歪みを帯びており、O2分子の拡散障壁が1.24eVから2.0eVに上がっているのだ、と主張しました。界面から約1nmの範囲のSiO2層は構造遷移領域と呼ばれ、この領域で密度が増加していることが以前より実験でも指摘されていました。
だとすると、Deal-Grove方程式の界面反応速度係数\(k\)も、SiO2膜厚が薄い初期段階のO2分子の拡散速度に関係していることになります。\(k\)が拡散係数\(D_0\)に関係しているとしたら、初期の異常な酸化速度の解釈も変わる可能性があります。
そこで筆者(渡邉)[3]は、界面近傍の構造遷移領域で局所的に拡散障壁が増加するというモデルを前提にして、Deal-Grove方程式に代わる新しい線形‐放物型方程式を導き、線形速度定数\(B/A\)を新たに定式化しました。新しい方程式を使って、線形速度定数\(B/A\)の実験値に合うような構造遷移領域の厚さを求めたところ、その厚さはおおむね1nm程度と算出されました。これは実験で指摘されていた構造遷移領域の厚さと一致します。そして予想通り、初期の異常な酸化速度も拡散速度の上昇で説明すべきであることが判明し、Fargeixらの解析[4]以来お蔵入りにされてきた「初期増速拡散説」が復活することがわかりました。
[1] A. Bongiorno, A. Pasquarello, Phys. Rev. Lett., 93, 086102 (2004).
[2] T. Akiyama and H. Kageshima, Surf. Sci., 576, L65 (2005).
[3] T. Watanabe, K. Tatsumura, I. Ohdomari, Phys. Rev. Lett., 96, 196102 (2006).
[4] A. Fargeix, G. Ghibaudo, G. Kamarinos, J. Appl. Phys. 54, 2878 (1983).
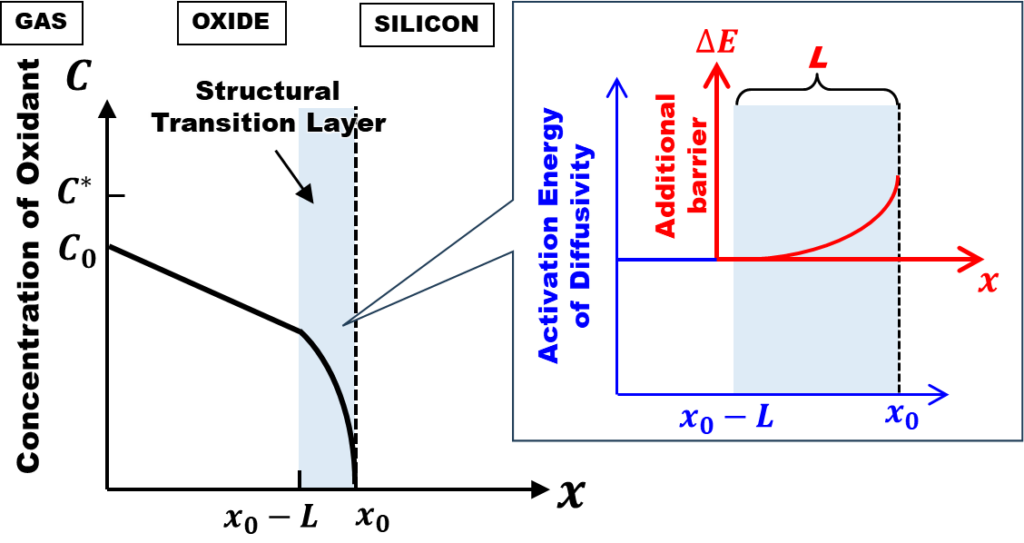
上図が、完全拡散律速熱モデルで想定するO2濃度プロファイルです。右側のグラフは、構造遷移領域におけるO2分子の拡散係数の活性化エネルギーの分布を示しています。Deal-Groveのような界面反応の障壁の代わりに、界面近傍の厚さLの構造遷移領域内で拡散障壁が上昇し、濃度が急低下していると考えるのです。
次回から、上図のモデルに基づく新しい酸化速度方程式の導出を示していきます。