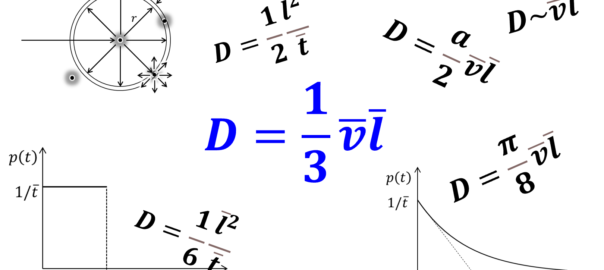渡邉孝信（早稲田大学・電子物理システム学科）

ボルツマン方程式から拡散係数を導く

　非平衡統計力学のボルツマン方程式を学ぶと、ドリフト移動度を定義しなくても、

$$\begin{array}{}\text{(3.1)}& D=\frac{1}{3}\bar{v}\bar{l}\end{array}$$

を比較的すっきりと導くことができます。ボルツマン方程式とは、空間座標$\mathit{r}$と運動量$\mathit{p}$の６次元の位相空間における、粒子系の分布関数$f(\mathit{r},\mathit{p},t)$についての微分方程式で、次式で与えられます。

$$\begin{array}{}\text{(3.2)}& \frac{\partial f}{\partial t}+\frac{\mathit{p}}{m}\cdot \frac{\partial f}{\partial \mathit{r}}+\mathit{F}\cdot \frac{\partial f}{\partial \mathit{p}}=-{\left(\frac{\partial f}{\partial t}\right)}_c\end{array}$$

$\mathit{F}$は粒子系に加わる外力、$-{\left(\frac{\partial f}{\partial t}\right)}_c$は衝突によって生じる変化、すなわち、微小領域$d\mathit{r}\mathit{p}d\mathit{p}$において微小時間$dt$に衝突によって生じる$f$の変化を表します。この衝突項$-{\left(\frac{\partial f}{\partial t}\right)}_c$を

$$\begin{array}{}\text{(3.3)}& -{\left(\frac{\partial f}{\partial t}\right)}_c=-\frac{f-f_0}{\tau }\end{array}$$

とするのが緩和時間近似です。$\tau$が緩和時間と呼ばれるパラメータで、$f_0$は熱平衡状態の分布関数を表します。今、外力$\mathit{F}$が加わっておらず、濃度の一様な系を仮定すると、式$\text{(3.2)}$において$\mathit{F}=\mathbf{0}$、$\frac{\partial f}{\partial \mathit{r}}=\mathbf{0}$とおけるので、

$$\begin{array}{}\text{(3.4)}& \frac{df}{dt}=-\frac{f-f_0}{\tau }\end{array}$$

が解くべき微分方程式となります。初期値$f(0)$を境界条件とする解は

$$\begin{array}{}\text{(3.5)}& f(t)=(f(0)–f_0)e^{-\frac{t}{\tau }}+f_0\end{array}$$

となり、時定数$\tau$で$f_0$に落ち着いていく、という解になります。

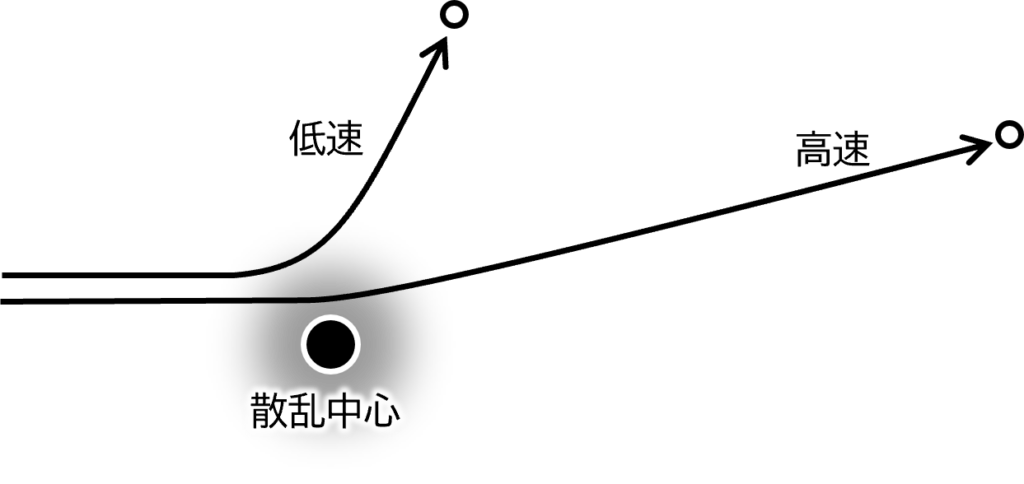
衝突が分布関数に与える影響は、本来、電子の運動エネルギーに依存するはずです。例えば、半導体中の電子が不純物イオンと衝突する場合、電子が速く動いている時はゆっくり動くときと比べて、不純物イオンの周辺のポテンシャルの影響は小さく、正面衝突するのでなければ、進路はそれほど大きく乱されません（図3.1参照)。よって緩和時間$\tau$は$\mathit{p}$の関数$\tau (\mathit{p})$とみなすべきです。それを無視して、緩和時間$\tau$を定数とおいてしまおうという、ざっくりした近似を、定緩和時間近似と呼びます。

 

　拡散電流は、分布関数が実空間上で一様でない場合に生じます。外力$\mathit{F}$がなく、濃度が一様でない状態で系が定常状態にあるとき、式$\text{(3.2)}$において$\mathit{F}=\mathbf{0}$、$\frac{\partial f}{\partial t}=0$とした

$$\begin{array}{}\text{(3.6)}& \frac{\mathit{p}}{m}\cdot \frac{\partial f}{\partial \mathit{r}}=-\frac{f-f_0}{\tau }\end{array}$$

の解を求めてみましょう。$\mathit{p}/m=\mathit{v}$として式変形すると

$$\begin{array}{}\text{(3.7)}& f(\mathit{r})=f_0(\mathit{r})-\tau \mathit{v}\cdot \frac{\partial f}{\partial \mathit{r}}\end{array}$$

となります。ここで、$\tau \mathit{v}$の大きさが十分小さく、解がべき級数

$$\begin{array}{}\text{(3.8)}& f=f_0-\tau \mathit{v}\cdot f_1+{(\tau \mathit{v})}^2{f}_2\cdots \end{array}$$

の形で表せると仮定して、$f_1,f_2,\cdots$を求めてみます。式$\text{(3.8)}$を式$\text{(3.7)}$に代入すると、

$$\begin{array}{}\text{(3.9)}& f_0-\tau \mathit{v}\cdot f_1+{(\tau \mathit{v})}^2{f}_2\cdots =f_0-\tau \mathit{v}\cdot \frac{\partial f_0}{\partial \mathit{r}}+{(\tau \mathit{v})}^2\frac{\partial f_1}{\partial \mathit{r}}\end{array}$$

となり、各次の項を比較すると

$$f_1=\frac{\partial f_0}{\partial \mathit{r}},f_2=\frac{\partial f_1}{\partial \mathit{r}},\cdots$$

と求まります。ここでは展開を１次で打ち切って、

$$\begin{array}{}\text{(3.10)}& f(\mathit{r})\cong f_0(\mathit{r})-\tau \mathit{v}\cdot \frac{\partial f_0}{\partial \mathit{r}}\end{array}$$

を近似解として採用しましょう。

　拡散電流$\mathit{J}$（正確には拡散電流密度。単位はA/cm${}^2$）を求めるには、運動量空間で$\mathit{v}f$を積分します。

$$\begin{array}{}\text{(3.11)}& \mathit{J}=-q\int \mathit{v}fd\mathit{p}=-q\int \left\{\mathit{v}{f}_0–\tau \mathit{v}(\mathit{v}\cdot \frac{\partial f_0}{\partial \mathit{r}})\right\}d\mathit{p}\end{array}$$

今、$f$の偏りが実空間の$x$方向にのみ一様に生じていると仮定すると、拡散電流は$x$成分のみとなり、

$$\begin{array}{}\text{(3.12)}& J_x=-q\int \left(v_x{f}_0–\tau v_x^2\frac{\partial f_0}{\partial x}\right)d\mathit{p}=-q\tau \overline{v_x^2}\frac{dn}{dx}\end{array}$$

となります。なお、ここでは分布関数が$f_0(\mathit{r},\mathit{p})=n(\mathit{r})g_0(\mathit{p})$と変数分離できると仮定し（$n(\mathit{r})$は実空間上の電子密度分布を表します）、

$$\begin{array}{}\text{(3.13)}& \overline{v_x}=\int v_x{g}_0(\mathit{p})d\mathit{p}=0\end{array}$$

$$\begin{array}{}\text{(3.14)}& \overline{v_x^2}=\int v_x^2{g}_0(\mathit{p})d\mathit{p}(=\frac{k_{B}T}{m})\end{array}$$

としています。$\overline{v_x^2}=\overline{v^2}/3$とおけるので

$$\begin{array}{}\text{(3.15)}& J_x=-q\frac{\tau \overline{v^2}}{3}\frac{dn}{dx}\end{array}$$

となり、これをフィックの法則

$$\begin{array}{}\text{(3.16)}& J_x=-qD\frac{dn}{dx}\end{array}$$

と比較すると、拡散係数$D$は

$$\begin{array}{}\text{(3.17)}& D=\frac{1}{3}\tau \overline{v^2}\end{array}$$

となります。緩和時間$\tau$を平均自由時間$\bar{t}$、根二乗平均速度$\sqrt{\overline{v^2}}$を平均熱速度$\bar{v}$とみなせば、$\bar{l}=\bar{v}\bar{t}$とおくことで、式$\text{(3.17)}$は式$\text{(3.1)}$と一致します。緩和時間$\tau$と平均自由時間$\bar{t}$は元来異なる概念ですが、１回の衝突で過去の履歴が完全に失われ速度分布がリセットされると仮定すると、両者は一致します（この仮定はよく設けられる仮定ですが、よくよく考えると、必ずしも妥当とは言い切れない仮定です）。

　念のため断っておきますが、「$D=\bar{v}\bar{l}/3$ が正しい」と言いたいのではありません。ボルツマン方程式の定緩和時間近似で導かれる拡散係数と整合する、と言いたいだけです。