力の計算ルーチンの記述
ボンドオーダー型のポテンシャルのインプリメントは大変そうに見えるかもしれないが、Stillinger-Weberポテンシャルの項でも説明してきたターム指向記述を心がければ、間違いを最小限に押さえながら着実にコーディングできる。
1. ポテンシャルエネルギーを計算するコードを記述する。
$$ \mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j \neq i} \bigl\{ V \;+\!\!=\; \frac{1}{2} f_C(r_{ij})\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ] \bigr \} $$
2. 力の計算コードを追記する。
$$ \begin{eqnarray}
&& \mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j\neq i} \bigl\{ V \;+\!\!=\; \frac{1}{2} f_C(r_{ij})\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ];\bigr . \\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_i \;+\!\!=\; – \frac{\partial}{\partial \boldsymbol{r}_i}\frac{1}{2} f_C(r_{ij})\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ];\\
&& \;\;\;\;\;\;\;\;\;\;\boldsymbol{F}_j \;+\!\!=\; – \frac{\partial}{\partial \boldsymbol{r}_j}\frac{1}{2} f_C(r_{ij})\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ];\\
& & \;\;\;\;\;\;\;\;\;\; \mathop{\large \Lambda}_{k \neq i,j} \bigl\{ \boldsymbol{F}_k \;+\!\!=\; – \frac{1}{2} f_C(r_{ij})f_A(r_{ij}) \frac{\partial b_{ij}}{\partial \boldsymbol{r}_k} \bigr \}\\
& & \bigl . \bigr \}
\end{eqnarray}$$
\(\large \Lambda\)という記号はforループを表す本稿オリジナルの記号である。ポイントは、\(\boldsymbol{F}_i\)と\(\boldsymbol{F}_j\)だけでなく、ボンドオーダー項\(b_{ij}\)に関与する周辺の全ての原子\(k\)についても、注目している項から生じる力\(\boldsymbol{F}_k\)を計算して加える点にある。この力はとかく見落としがちでなので、筆者は個人的にextra forcesと呼んで注意を払っている。ポテンシャルの定義に立ち返り、extra forcesをしっかり列挙し尽くせば、MD計算をしたときにHamiltonianがきちんと保存される。
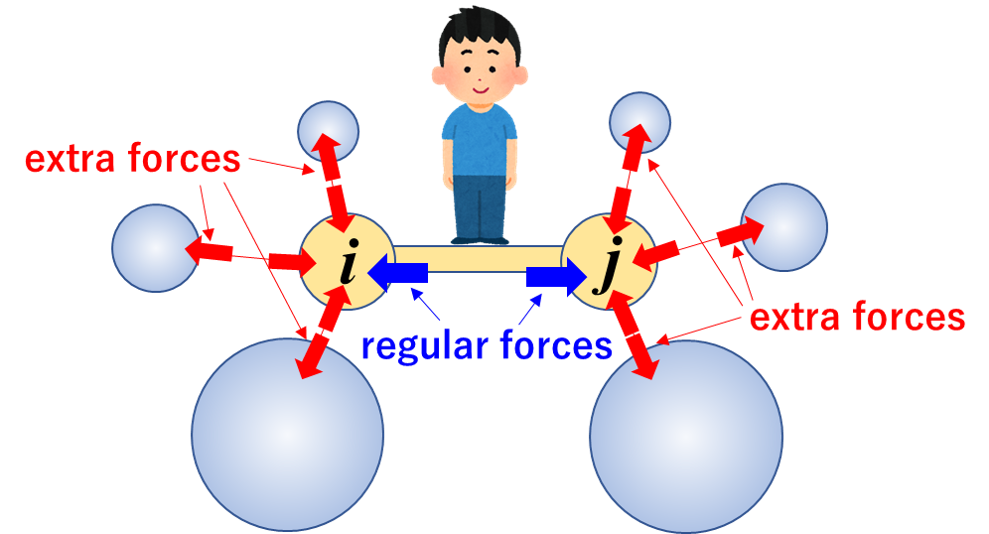
ここまでプログラムの枠組みができてしまえば、後は、煩雑ではあるが、一本道である(以下の式は未検証なので読者の責任においてご利用ください)。
$$ \begin{eqnarray}
& = & \mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j\neq i} \bigl\{ V \;+\!\!=\; \frac{1}{2} f_C(r_{ij})\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ];\bigr . \\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_i \;+\!\!=\; – \frac{1}{2}\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ]\frac{\partial f_C(r_{ij})}{\partial r_{ij}}\frac{\boldsymbol{r}_i – \boldsymbol{r}_j}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_i \;+\!\!=\; – \frac{1}{2}f_C(r_{ij})\left [ \frac{\partial f_R(r_{ij})}{\partial r_{ij}} + b_{ij}\frac{\partial f_A(r_{ij})}{\partial r_{ij}}\right ] \frac{\boldsymbol{r}_i – \boldsymbol{r}_j}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_i \;+\!\!=\; – A_{ij} \sum_{k \neq i,j} B_{jik} \frac{\boldsymbol{r}_i – \boldsymbol{r}_j}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_i \;+\!\!=\; – A_{ij} \sum_{k \neq i,j} C_{jik} \frac{\boldsymbol{r}_i – \boldsymbol{r}_k}{r_{ik}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_j \;+\!\!=\; -\frac{1}{2}\left [ f_R(r_{ij})+b_{ij}f_A(r_{ij})\right ]\frac{\partial f_C(r_{ij})}{\partial r_{ij}}\frac{\boldsymbol{r}_j – \boldsymbol{r}_i}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_j \;+\!\!=\; -\frac{1}{2}f_C(r_{ij})\left [ \frac{\partial f_R(r_{ij})}{\partial r_{ij}} + b_{ij}\frac{\partial f_A(r_{ij})}{\partial r_{ij}}\right ] \frac{\boldsymbol{r}_j – \boldsymbol{r}_i}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_j \;+\!\!=\; – A_{ij} \sum_{k \neq i,j} B_{jik} \frac{\boldsymbol{r}_j – \boldsymbol{r}_i}{r_{ij}};\\
&& \;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_j \;+\!\!=\; – A_{ij} \sum_{k \neq i,j} D_{jik} \frac{\boldsymbol{r}_j – \boldsymbol{r}_k}
{r_{jk}};\\
& & \;\;\;\;\;\;\;\;\;\; \mathop{\large \Lambda}_{k \neq i,j} \bigl\{ \bigr .\\
& & \;\;\;\;\;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_k \;+\!\!=\; – A_{ij} C_{jik} \frac{\boldsymbol{r}_k – \boldsymbol{r}_i}{r_{ik}};\\
& & \;\;\;\;\;\;\;\;\;\;\;\;\;\; \boldsymbol{F}_k \;+\!\!=\; – A_{ij} D_{jik} \frac{\boldsymbol{r}_k – \boldsymbol{r}_j}
{r_{jk}};\\
&& \;\;\;\;\;\;\;\;\;\; \bigl . \bigr \}\\
& & \bigl . \bigr \}
\end{eqnarray}$$
ここで
$$
\begin{eqnarray}
A_{ij} &=& \frac{1}{2}f_C(r_{ij})f_A(r_{ij})\frac{\partial b_{ij}}{ \partial \zeta_{ij}}\\
B_{jik} &=& f_C(r_{ik})\exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ]\frac{\partial g(\theta_{ijk})}{\partial \cos\theta_{jik}}\frac{r_{ij} – r_{ik}\cos\theta_{jik}}{r_{ij}r_{ik}} \\
&&+ 3\lambda^3_3 {(r_{ij}-r_{ik})}^2f_C(r_{ik}) g(\theta_{jik})\exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ]\\
C_{jik} &=& g(\theta_{jik})\exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ]\frac{\partial f_C(r_{ik})}{\partial r_{ik}}\\
&& + f_C(r_{ik})\exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ] \frac{\partial g(\theta_{jik})}{\partial \cos\theta_{jik}}\frac{r_{ik} – r_{ij}\cos\theta_{jik}}{r_{ij}r_{ik}}\\
&& – 3 \lambda^3_3 {(r_{ij}-r_{ik})}^2f_C(r_{ik}) g(\theta_{jik})\exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ]\\
D_{jik} &=&- f_C(r_{ik}) \exp [ \lambda^3_3 {(r_{ij}-r_{ik})}^3 ] \frac{\partial g(\theta_{ijk})}{\partial \cos\theta_{ijk}}\frac{r_{jk}}{r_{ij}r_{ik}}
\end{eqnarray}
$$
とおいた。
作用-反作用の法則に従い、大きさが同じで反対向きの力が必ず相手の原子にも働いていることに注目しよう。この作用-反作用の法則はデバグに利用できる上、共通する項をメモリに格納しておくことで計算量を減らすことにも使える。