今回は、Deal-Grove方程式を導出します。ちゃんと勉強するなら、Deal-Groveの原著論文¹⁾や、Grove自身が書いた教科書²⁾を読んだ方がずっと近道なのですが、この後の記事とのつながりもありますので、簡単に説明しておきます。

導出の方針

Si表面の酸化は、雰囲気中の酸化種分子（O₂分子やH₂O分子）がSiO₂膜に浸透してSi基板に達し、SiO₂/Si界面で酸化反応を起こす、という流れで進みます。このことは同位体をマーカーとして使った実験で確認されています。

ただし、Si原子が全く動かないわけではなく、Si基板からSi原子が放出されてSiO₂膜中を拡散し、SiO₂面膜中やSiO₂表面で酸化種分子と出合って酸化反応が起きるという説³⁾もあります。ドライ酸化に見られる初期の異常な酸化速度は、このSi原子放出が原因だというのです。ただしこの説でも、Si原子の放出量は少量で、SiO₂膜の大部分はSiO₂/Si界面で形成されると考えられています。よって、おおよその酸化速度は、酸化種分子の輸送プロセスだけ考えれば記述できます。

さて、酸化種分子がSiO₂/Si界面に到達してSi基板を酸化するまでには、次の３つの過程を経る必要があります。

• 第１段階：気相雰囲気中の酸化種分子がSiO₂膜表面に到達する過程。
• 第２段階：酸化種分子が既に存在するSiO₂膜中を拡散する過程。
• 第３段階：SiO₂/Si界面に到達した酸化種分子がSi基板を酸化して消費される過程。

以上の３つの段階に対応する酸化種分子の流束（単位時間あたりに単位断面積を通過する酸化種分子数）を$F_1$、$F_2$、$F_3$と表記し、それぞれを定式化してみましょう。

第１段階：$F_1$の定式化

気相中の酸化種分子の流束は、気相中の酸化種の濃度$C_G$とSiO₂膜表面ごく近傍における酸化種の濃度$C_S$の差に比例する線形近似で表すことができます。

$$F_1=h_G(C_G–C_S)$$

ここで$h_G$は気相中の物質輸送係数です。この式の中の、気相の酸化種の濃度$C_G$と$C_S$を、酸化膜中の酸化種の濃度で置き換えることを考えてみましょう。

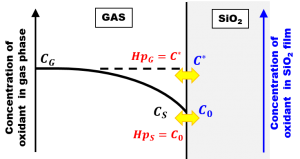
一般に、溶液中に溶け込んだ溶質の濃度が薄い場合、溶質の濃度は気体中のその物質の分圧に比例することが知られています。Henryの法則です。今考えている系は固体ですが、SiO₂膜中に含まれる酸化種にこのHenryの法則を適用すると、表面近傍の酸化種の濃度$C_0$は、定常状態ではSiO₂膜表面ごく近傍における酸化種の分圧$p_S$に比例すると考えられます。

$$C_0=H{p}_S$$

ここで$H$はHenryの法則における比例定数です。同様に、SiO₂膜中の酸化種の平衡濃度$C^{\ast }$は、気相中の酸化種の分圧$p_G$と

$$C^{\ast }=H{p}_G$$

で関係づけられます。

理想気体の状態方程式

$$p_G=C_G{k}_{B}T$$

$$p_S=C_S{k}_{B}T$$

より、気相中の酸化種分子の流束$F_1$は、

$$F_1=\frac{h_G}{H{k}_{B}T}(C^{\ast }–C_0)\equiv h(C^{\ast }–C_0)$$

と表されます。$h$は言うなれば、SiO₂膜中の酸化種濃度で表した場合の気相物質輸送係数、ということになります。

第２段階：$F_2$の定式化

SiO₂膜中を拡散する酸化種の流束$F_2$は、Fickの第一法則より

$$F_2=-D_0\frac{dC(x)}{dx}$$

で与えられます。$D_0$はSiO₂膜中の酸化種分子の拡散係数です。SiO₂膜中の酸化種の濃度勾配は

$$\frac{dC(x)}{dx}=\frac{C_i-C_0}{x_0}$$

で表されるので、

$$F_2=-D_0\frac{C_i-C_0}{x_0}$$

となります。

第３段階：$F_3$の定式化

界面に到達した酸化種分子が酸化反応で消費される速度は、界面の酸化種濃度に比例すると考えられます。よって、界面における酸化反応速度定数を$k$と書くと、

$$F_3=k{C}_i$$

と与えられます。

Deal-Grove方程式の導出

定常状態を考えると、上記の３つの段階に対応する酸化種分子の流束$F_1$、$F_2$、$F_3$はつり合っていると考えられます。よって$F\equiv F_1=F_2=F_3$の条件を課すと、定常状態の流束$F$は

$$F=\frac{D_0{C}^{\ast }}{D_0(1/k+1/h)+x_0}$$

と与えられます。これが、界面の単位面積で単位時間に消費される酸化種分子の個数となります。SiO₂膜の成長速度、すなわち、SiO₂膜の厚さ$x_0$が増える速度は、この流束$F$に比例することになります。

SiO₂膜の単位体積当たりに取り込まれる酸化種分子の個数を$N_1$とおくと、

$$\frac{d{x}_0}{dt}=\frac{F}{N_1}=\frac{D_0{C}^{\ast }/N_1}{D_0(1/k+1/h)+x_0}$$

という、SiO₂膜厚$x_0$の時間に関する微分方程式が得られます。これがDeal-Grove方程式です。

以後、この微分方程式を下記のように簡略化して表記します。

$$\frac{d{x}_0}{dt}=\frac{B}{A+2x_0}$$

ここで

$$A=2D_0(1/k+1/h)$$

$$B=2D_0{C}^{\ast }/N_1$$

です。わざわざ分子と分母を２倍した理由は、こうしておくとこの後で求める微分方程式の解がシンプルに表記できるからです。

1. B. E. Deal, A. S. Grove, J. Appl. Phys. 36, 3770 (1965).
2. 垂井康夫 監訳, Andrew. S. Grove著, “グローブ 半導体デバイスの基礎,” オーム社 (1995).
3. H. Kageshima, K. Shiraishi, M. Uematsu, Jpn. J. Appl. Phys., 38, L971, (1999).