Lennard-Jonesポテンシャルを用いたMD計算
1. VC++で下記のプログラムを作成する。
#include <stdafx.h>;
#include <stdlib.h>;
#include <math.h>;
#define N 125
#define ROW 5 // ROW^3 = N
#define INTERVAL 3.4
int _tmain(int argc, _TCHAR* argv[])
{
double rx[N], ry[N], rz[N]; // coordinates
double rxb[N], ryb[N], rzb[N]; // coordinates at previous step
double rxc[N], ryc[N], rzc[N]; // coordinates at two steps before
double vx[N], vy[N], vz[N]; // velocity
double fx[N], fy[N], fz[N]; // force components
double m[N]; // atomic mass
double sigma, epsilon; // Lennard-Jones potential parameters
double rij, fij, tmp; // separation, force, temporal memory
double dxij, dyij, dzij; // relative position vector
double t, dt; // duration, time step
double K; // kinetic energy
double V; // potential energy
int i,j,k,l;
FILE *fp;
FILE *fpdata;
fopen_s(fp, "LJ125atoms.xyz");
if(fp == NULL){
printf("ERROR: File open failed.\n"); exit(1);
}
fopen_s(fpdata, "LJ125atoms.csv");
if(fpdata == NULL){
printf(&quot;ERROR: File open failed.\n&quot;); exit(1);
}
fprintf(fpdata,"time,kinetic energy,potential energy,Hamiltonian\n");
// Initialization
dt = 0.005;
for(i=0; i<N; ++i){
m[i] = 1.0;
}
sigma = 3.41; epsilon = 119.8;
i = 0;
for(j=0; j<ROW; ++j){
for(k=0; k<ROW; ++k){
for(l=0; l<ROW; ++l){
rx[i] = 0.5 + INTERVAL * j;
ry[i] = 0.5 + INTERVAL * k;
rz[i] = 0.5 + INTERVAL * l;
rxb[i] = rx[i];
ryb[i] = ry[i];
rzb[i] = rz[i];
++i;
}
}
}
for(t=0.0; t<2.0; t+=dt){
// force and potential energy calculation
V =0.0; K = 0.0;
for(i=0; i<N; ++i){
fx[i] = 0.0; fy[i] = 0.0; fz[i] = 0.0;
}
for(i=0; i<N; ++i){
for(j = i+1; j<N; j++){
dxij = rx[i] - rx[j];
dyij = ry[i] - ry[j];
dzij = rz[i] - rz[j];
rij = sqrt(dxij * dxij + dyij * dyij + dzij * dzij);
fij = - 4.0 * epsilon *(-12.0 * pow(sigma/rij, 12.0) / rij
+ 6.0 * pow(sigma/rij, 6.0) / rij);
fx[i] += fij * dxij / rij;
fy[i] += fij * dyij / rij;
fz[i] += fij * dzij / rij;
fx[j] -= fij * dxij / rij;
fy[j] -= fij * dyij / rij;
fz[j] -= fij * dzij / rij;
V += 4.0*epsilon*(pow(sigma/rij,12.0)-pow(sigma/rij,6.0));
}
}
// the Verlet algorithm
for(i=0; i<N; ++i){
rxc[i] = rxb[i];
tmp = rx[i];
rx[i] = 2.0 * rx[i] - rxb[i] + dt * dt * fx[i] / m[i];
rxb[i] = tmp;
ryc[i] = ryb[i];
tmp = ry[i];
ry[i] = 2.0 * ry[i] - ryb[i] + dt * dt * fy[i] / m[i];
ryb[i] = tmp;
rzc[i] = rzb[i];
tmp = rz[i];
rz[i] = 2.0 * rz[i] - rzb[i] + dt * dt * fz[i] / m[i];
rzb[i] = tmp;
}
// kinetic energy calculation
for(i=0; i<N; ++i){
vx[i] = (rx[i] - rxc[i]) / (2.0 * dt);
vy[i] = (ry[i] - ryc[i]) / (2.0 * dt);
vz[i] = (rz[i] - rzc[i]) / (2.0 * dt);
K += 0.5 * m[i] * (vx[i]*vx[i]+vy[i]*vy[i]+vz[i]*vz[i]);
}
// print time, kinetic energy, potential energy and Hamiltonian
fprintf(fpdata,"%f,%f,%f,%f\n",t,K,V,K+V);
// print structure
fprintf(fp, "%d\n", N);
fprintf(fp, "Lennard Jones potential\n");
for(i=0; i<N; ++i){
fprintf(fp, "Ar %f %f %f\n", rx[i], ry[i], rz[i]);
}
}
fclose(fp);
fclose(fpdata);
return 0;
}
2.ビルド、実行
- プログラムをビルド、実行すると、プロジェクト・ディレクトリの中の、プロジェクト名と同じディレクトリの中に“LJ125atoms.xyz”というファイルと“LJ125atoms.csv” というファイルが生成される。
- “LJ125atoms.csv”に、運動エネルギー、ポテンシャルエネルギー、ハミルトニアンの時間変化が記録されている。
3. VMDでアニメーションを表示
- VMDで“LJ125atoms.xyz”を読み込み、アニメーションを表示する。
- 「Graphics Representation」ダイアログの「Drawing Method」で「VDW」を選択する。
- 下図のような125原子系の分子動力学計算の結果が表示される。
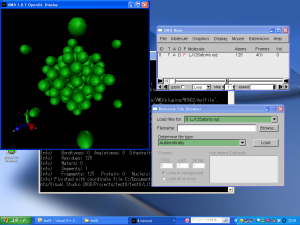 Lennard-Jonesポテンシャルを用いたMDシミュレーションの結果(Ar原子125個)
Lennard-Jonesポテンシャルを用いたMDシミュレーションの結果(Ar原子125個)
4. 運動エネルギー、ポテンシャルエネルギー、ハミルトニアンの表示
- Excelで“LJ125atoms.csv”を開き、運動エネルギー、ポテンシャルエネルギー、ハミルトニアンの時間変化のグラフを表示してみよう。
- ハミルトニアンがほぼ一定に保たれていることを確認しよう。
