繰り返し手続きを表す記法の導入

forループのプログラム

for(i=0; i<N; i++){
  a[i] += f();
}

を次のように記述してみよう。

$$ \mathop{\large \Lambda}_{i=0}^{N-1} \Bigl\{a_i \;+\!\!=\; f() \Bigr\}$$

ここで\(\Lambda\)は本稿オリジナルの記法で、右に書かれている代入操作を\(i=0\)から\(i=N-1\)まで\(i\)を1つずつ増やしながら繰り返し実行することを表す。操作の結果が繰り返しの順序によらない場合は交換則

$$ \mathop{\large \Lambda}_{i}\mathop{\large \Lambda}_{j}\bigl\{{\it operation}\bigr\} = \mathop{\large \Lambda}_{j}\mathop{\large \Lambda}_{i}\bigl\{{\it operation}\bigr\} $$

が成り立つ。等号は「計算で扱っている変数の値が、一連の計算終了後に全て同じになる」ことを意味する。

また、原子間ポテンシャルや力の計算でよく現れる和\(\sum\)は、繰り返しの足し算操作であるから

$$ \mathop{\large \Lambda}_{i}\left\{a_i\;+\!\!=\;\sum_j f_j\right\} = \mathop{\large \Lambda}_{i}\mathop{\large \Lambda}_{j}\Biggl\{a_i\;+\!\!=\;\ f_j\Biggr\} $$

のように\(\Lambda\)を使って書き直すことができる。

 アトム指向記述とターム指向記述

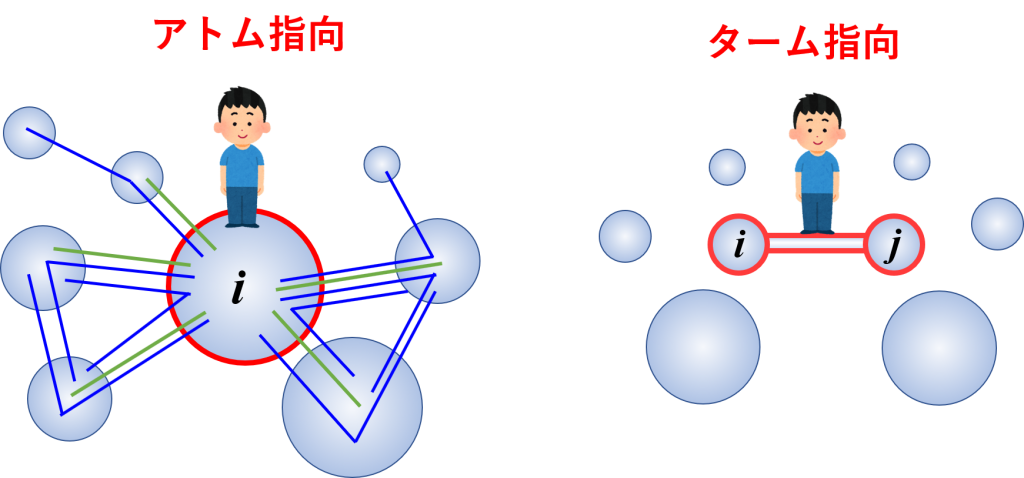
アトム指向記述とターム指向記述のイメージ図。アトム指向では１つの原子に注目し、その原子が関わる全てのポテンシャル項（ターム）を列挙して力を計算する。一方、ターム指向では、１つのポテンシャル項に注目し、その項に関わる全ての原子を列挙して、そのポテンシャル項から生じる力を各原子に配分していく。ターム指向で記述した方が数え落としの恐れが少なく、計算速度も上げやすい。

forループによる繰り返し操作を表す\(\Lambda\)を使って、Lennard-Jonesポテンシャル

$$ V = \sum _i \sum_{j>i} v_2^{\rm LJ}(r_{ij}) = \sum _i \sum_{j>i} 4 \varepsilon \left \{ \left ( \frac{\sigma}{r_{ij}} \right )^{12} – \left ( \frac{\sigma}{r_{ij}} \right )^6 \right \} $$

とその力

$$ \boldsymbol{F}_i = -\sum_{j\neq i} 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}
^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_i-\boldsymbol{r}_j}{r_{ij}}
$$

の計算ルーチンを記述してみよう。

ポテンシャルエネルギーの計算ルーチンは

$$ \mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j>i} \Biggl\{ V \;+\!\!=\; 4 \varepsilon \left \{ \left ( \frac{\sigma}{r_{ij}} \right )^{12} – \left ( \frac{\sigma}{r_{ij}} \right )^6 \right \} \Biggr\}$$

でよい。これは問題ないだろう。

力については、系の全ての原子にかかる力を計算するのだから、

$$ \begin{eqnarray}
&&\mathop{\large \Lambda}_{i} \Biggl\{ \boldsymbol{F}_i \;+\!\!=\; -\sum_{j\neq i} 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_i-\boldsymbol{r}_j}{r_{ij}} \Biggr\}\\
&=& \mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j\neq i} \Biggl\{ \boldsymbol{F}_i \;+\!\!=\; – 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}
^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_i-\boldsymbol{r}_j}{r_{ij}} \Biggr\}
\end{eqnarray}
$$

となる。これをアトム指向記述と筆者は呼んでいる。ポテンシャルの計算も一緒に行うなら、

$$ \begin{eqnarray}
&\mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j \neq i} \bigl\{ \bigr .&\\
&& {\rm if}(j>i) \;\;\; V \;+\!\!=\; 4 \varepsilon \left \{ \left ( \frac{\sigma}{r_{ij}} \right )^{12} – \left ( \frac{\sigma}{r_{ij}} \right )^6 \right \} ;\\
&& \boldsymbol{F}_i \;+\!\!=\; – 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}
^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_i-\boldsymbol{r}_j}{r_{ij}}\\
&\bigl . \bigr \}&
\end{eqnarray}$$

と記述すればよい。\(j\)についての\(\Lambda\)ループの範囲が\(j > i\)に限定されていないので、\( {\rm if}(j>i)\)の制限がないとポテンシャルエネルギーを足し合わせすぎることになる。Lennard-Jonesポテンシャルは単純だから問題ないかもしれないが、３体項など複雑な項を含むポテンシャルの場合は、どのような制限を設けたらよいか分かりにくくなり、ミスの原因になりやすい。

これに対しターム指向記述では、ポテンシャルの計算ルーチンをベースに力の計算手続きを加えていく。

$$ \begin{eqnarray}
&\mathop{\large \Lambda}_{i} \mathop{\large \Lambda}_{j>i} \bigl\{ \bigr .&\\
&& V \;+\!\!=\; 4 \varepsilon \left \{ \left ( \frac{\sigma}{r_{ij}} \right )^{12} – \left ( \frac{\sigma}{r_{ij}} \right )^6 \right \} ;\\
&& \boldsymbol{F}_i \;+\!\!=\; – 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_i-\boldsymbol{r}_j}{r_{ij}};\\
&& \boldsymbol{F}_j \;+\!\!=\; – 4 \varepsilon \left ( -12 \frac{\sigma^{12}}{r_{ij}^{13}} + 6 \frac{\sigma^6}{r_{ij}^7} \right)\frac{\boldsymbol{r}_j-\boldsymbol{r}_i}{r_{ij}}\\
&\bigl . \bigr \}&
\end{eqnarray}$$

ターム指向記述のポイントは、\(\Lambda\)ループの中の各ポテンシャルエネルギー項に注目し、その項に関与する全ての原子（ここでは\(i\)と\(j\)の２個）に掛かる力を計算して足し合わせている点にある。まず系の全ポテンシャルエネルギーを計算するルーチンを記述しておき、このフレームワークの中で、力の計算式を追記するだけでよい。

ここで取り上げたLennard-Jonesポテンシャルは非常に単純なので、ターム指向記述の良さは伝わりにくいかもしれない。ターム指向記述の良さは、より複雑なポテンシャルでも、同じ手順で機械的にポテンシャルエネルギーと力の計算ルーチンを作成できる点にある。作用-反作用の法則より原子\(i\)と原子\(j\)の間には逆向きに同じ大きさの力が働くから、うまく書けばアトム指向記述に比べて計算量を大幅に減らすことができる。

力の計算ルーチンをインプリメントする際は、ターム指向記述を心がけよう！